1. NHẬN BIẾT (5 câu)

Câu 1: Trong các biểu thức sau, biểu thức nào là đơn thức?

-1;      (x + 1).x ;   $(\sqrt{5}-1+x).y$ ;   $\frac{1}{2} xy^{2}$;   $\frac{x}{y}$ ;    $\frac{x}{2}.\sqrt{2}$;     $\frac{x}{2}.(3-\sqrt{2})$;   $-\pi .r^{2}$;   0;     

Giải:

Các biểu thức là đơn thức là: -1;$\frac{1}{2}xy^{2}$ ;$\frac{x}{2}.\sqrt{2}$ ;$-\pi .r^{2}$ ; 0.   

Câu 2: Thu gọn và tính giá trị của mỗi đơn thức sau

a) A =$\frac{1}{3}xy^{2}.(-2.x^{2}.y)$ biết x = -1; y = 1

b) B = $-2xy^{2}z.\frac{3}{4}x^{2}.y.z^{3}$ khi x = 1; y = 0,5; z = 2

Giải:

a) A =$\frac{1}{3}xy^{2}.(-2.x^{2}.y)$=$\frac{-2}{3}x^{3}y^{3}$

Thay x = -1 và y = 1 vào A ta được:

A = $\frac{-2}{3}(-1)^{3}.1^{3}=\frac{2}{3}$

b) B = $-2xy^{2}z.\frac{3}{4}x^{2}.y.z^{3}$ = $-2.\frac{3}{4}.(x.x^{2}).(y^{2}.y).(z.z^{3})=-\frac{3}{2}.x^{3}.y^{3}.z^{4}$

Thay x = 1; y = 0,5; z =  2 vào B ta được:

B =$-\frac{3}{2}.1^{3}.0,5^{3}.2^{4}$ = -3

Câu 3: Cho các đơn thức:

$A=(5-\sqrt{5})xyz$; $B=\frac{1}{5}x.y^{3}.\frac{2}{3}x^{2}z$; $C=(-\frac{3}{5}x^{5}.y^{3}).(-xy^{2}).\frac{2}{5}x^{2}y$  ;$D=15,25x.y^{3}.z^{2}$

a) Liệt kê các đơn thức thu gọn trong các đơn thức đã cho và thu gọn các đơn thức còn lại.

b) Với mỗi đơn thức nhận được, hãy cho biết hệ số, phần biến và bậc của nó.

 Giải:

a) Các đơn thức đã thu gọn là: $A=(5-\sqrt{5})xyz$;

$D=15,25x.y^{3}.z^{2}$;   

$B=\frac{1}{5}x.y^{3}.\frac{2}{3}x^{2}z=\frac{2}{15}.x^{3}.y^{3}.z$

$C=(-\frac{3}{5}x^{5}.y^{3}).(-xy^{2}).\frac{2}{5}x^{2}y$

$=\frac{-6}{25}.(x^{5}.x.x^{2}).(y^{3}.y^{2}.y)$

$=\frac{-6}{25}.x^{8}.y^{6}$

b) $A=(5-\sqrt{5}xyz)$

+ Hệ số: $5-\sqrt{5}$

+ Phần biến: xyz

+ Bậc: 3

$B=\frac{2}{15}.x^{3}.y^{3}.z$

+ Hệ số: $\frac{2}{15}$

+ Phần biến: $x^{3}.y^{3}.z$

+ Bậc: 7

$c=\frac{-6}{25}.x^{8}.y^{6}$

+ Hệ số: $\frac{-6}{25}$

+ Phần biến: $x^{8}.y^{6}$

+ Bậc: 14

$D=15,25x.y^{3}.z^{2}$

+ Hệ số: 15,25

+ Phần biến: $x.y^{3}.z^{2}$

+ Bậc: 6

Câu 4: Sắp xếp các đơn thức sau thành từng nhóm, mỗi nhóm chứa tất cả các đơn thức đồng dạng với nhau

$xy^{2}z^{2}$;$1,5x^{2}y^{3}$ ;$4xyz^{3}$ ;$-3xy^{2}z^{2}$ ;$\frac{4}{5}xyz^{3}$ ;$-5xyz^{3}$ ;$-x^{2}y^{3}$

Giải:

Nhóm các đơn thức đồng dạng với nhau là:

Câu 5: Rút gọn rồi tính giá trị của biểu thức

 $S=-5xy^{2}z+3xy^{2}z$ khi x = -2 ; y =-1; z = 4

Giải:

$S= -5xy^{2}z+3xy^{2}z=-2xy^{2}z$

Tại x = -2; y = -1 và z = 4 ta có:

$S=-2.(-2)(-1)^{2}.4=16$

2. THÔNG HIỂU (5 câu)

Câu 1. Các đơn thức trong mỗi trường hợp sau có đồng dạng hay không? Vì sao?

a) $x^{2}y^{4}$; $-3x^{2}y^{4}$ và $\sqrt{5}x^{2}y^{4}$
b) $x^{2}y^{2}z^{2}$ và $2x^{2}y^{2}z^{3}$

Giải:

a) Ba đơn thức $x^{2}y^{4}$; $-3x^{2}y^{4}$ và $\sqrt{5}x^{2}y^{4}$ đồng dạng vì chúng có hệ số khác 0 và cùng phần biến $x^{2}y^{4}$.
b) Hai đơn thức $x^{2}y^{2}z^{2}$ và $2x^{2}y^{2}z^{3}$ không đồng dạng vì chúng không có cùng phần biến.

Câu 2. Tính tổng của các đơn thức sau:

$-x^{2}y^{3}z^{4}$; $-\frac{1}{3}x^{2}y^{3}z^{4}$ ; $\frac{1}{5}x^{3}y^{5}$; $-6x^{3}y^{5}$; $\frac{3}{5}x^{3}y^{5}$;

Giải:

 $-x^{2}y^{3}z^{4}+(-\frac{1}{3}x^{2}y^{3}z^{4})+\frac{1}{5}x^{3}y^{5}+(-6x^{3}y^{5})+ \frac{3}{5}x^{3}y^{5}$

$=\left [ -x^{2}y^{3}z^{4}+\left ( -\frac{1}{3}x^{2}y^{3}z^{4} \right ) \right ] + \left [ \frac{1}{5}x^{3}y^{5}+\left ( -6x^{3}y^{5}+\frac{3}{5}x^{3}y^{5} \right ) \right ]$

$=-\frac{4}{5}x^{2}y^{3}z^{4}-\frac{24}{5}x^{3}y^{5}$

Câu 3: Thực hiện phép tính:

a) $3x^{2}y^{3}+4x^{2}y^{3}$
b)$4x^{3}y^{2}-7x^{3}y^{2}$
c)$8xy^{3}+xy^{3}$

Giải:

a) $3x^{2}y^{3}+4x^{2}y^{3}=7x^{2}y^{3}$
b) $4x^{3}y^{2}-7x^{3}y^{2}=-3x^{3}y^{2}$
c) $8xy^{3}+xy^{3}=9xy^{3}$

Câu 4: Thực hiện phép tính:

a) $9x^{3}y^{6}+4x^{3}y^{6}+7x^{3}y^{6}$
b) $9x^{5}y^{6}-14x^{5}y^{6}+5x^{5}y^{6}$

Giải:

a) $9x^{3}y^{6}+4x^{3}y^{6}+7x^{3}y^{6}=20x^{3}y^{6}$
b)  $9x^{5}y^{6}-14x^{5}y^{6}+5x^{5}y^{6}=0$

Câu 5: Mỗi cặp đơn thức sau có đồng dạng không? Nếu có, hãy tìm tổng và hiệu của chúng.

a) $4xy^{3}$ và $7xy^{3}$
b) xyz và $-3x^{2}y$
c) 2xy và $xyz^{2}$

 Giải:

a) $4xy^{3}$ và $7xy^{3}$ là hai đơn thức đồng dạng, vì có hệ số khác 0 và cùng phần biến là . Ta có:

 $4xy^{3}+7xy^{3}=11xy^{3}$

$4xy^{3}-7xy^{3}=-3xy^{3}$

b) Ta có xyx = xxy = $x^{2}y$

Vậy hai đơn thức xyx và $-3x^{2}y$ có hệ số khác 0 và cùng phần biến $x^{2}y$, do đó chúng ta là hai đơn thức đồng dạng. Ta có:

xyx + $(-3xy^{3})=x^{2}y-3x^{2}y=-2x^{2}y$

xyx - $(-3xy^{3})=x^{2}y+3x^{2}y=4x^{2}y$

c) Ta thấy đơn thức $xyz^{2}$ chứa biến z, trong khi đơn thức 2xy không chứa biến z, do đó chúng ta phần biến khác nhau. Bởi vậy, chúng không phải là hai đơn thức đồng dạng.

3. VẬN DỤNG (5 câu)

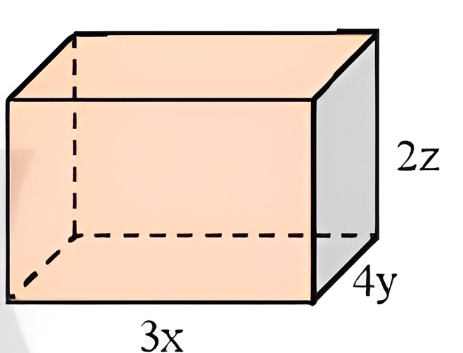
Câu 1: Viết biểu thức biểu thị thể tích V của hình hộp chữ nhật trong hình.

Giải:

- Biểu thức biểu thị thể tích V của hình hộp chữ nhật trong hình sau:

V = 3x. 4y. 2z = 24xyz (dvtt)

Câu 2: Viết biểu thức tính diện tích hình vuông biết độ dài một cạnh hình vuông là 5a.

Giải:

- Biểu thức tính diện tích hình vuông là:

S = 5a.5a = 25a² (dvdt)

Câu 3: Viết biểu thức tính diện tích hình chữ nhật S biết chiều dài là 5a và chiều rộng là 6b. Tính giá trị của S biết a = 1, b = 0,5.

Giải:

- Biểu thức tính diện tích hình chữ nhật là:

S = 5a.6b = 30ab (dvdt)

Tại a = 1; b = 0,5 ta có:

S =  30.1.0,5 = 5 (dvdt)

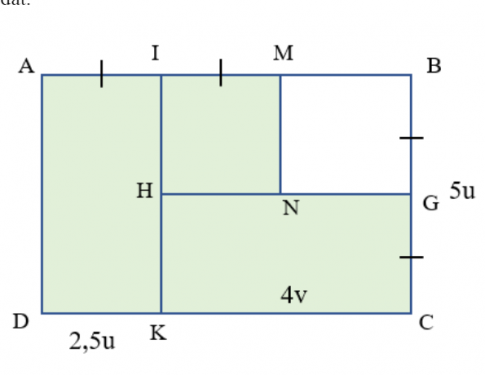
Câu 4. Một mảnh đất có dạng như phần được tô màu trong hình vẽ cùng các kích thước được ghi trên đó. Hãy tìm đơn thức (thu gọn) với hai biến x và y biểu thị diện tích của mảnh đất.

Giải:

Diện tích mảnh đất là:

S =  S_AIKD + S_IMNH + S_HGCK = 2,5u. 5u + 2,5u.2,5u + 2,5u.4v

= 12,5u² + 6,25u² + 10uv

= 18,75u² + 10uv (dvdt)

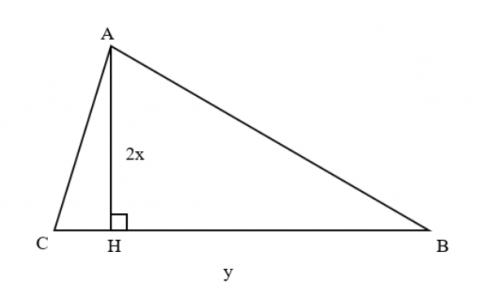
Bài 5. Tìm đơn thức biểu thị diện tích tam giác và tính diện tích tam giác ACB biết x = 2; y = 5

Giải:

Diện tích tam giác ABC là:

S = = x.y (dvdt)

Tại x = 2 và y = 5 ta có:

S = 2.5 = 10 (dvdt)

4. VẬN DỤNG CAO (4 câu)

Câu 1: Cho 3 đơn thức: $3a^{2}x^{m}y^{n-1}$; $\frac{2}{15}b^{2}.x^{n}.y^{m-3}$; $-2,5c^{2}.x^{m-2n}.y^{3}$; với a, b, c là các hằng số, m;n là các số tự nhiên.Tìm tích P của 3 đơn thức trên.

Giải:

P = $3a^{2}x^{m}y^{n-1}.\frac{2}{15}b^{2}.x^{n}.y^{m-3}.(-2,5c^{2}.x^{m-2n}y^{3})$

= $\left [ 3.a^{2}.\frac{2}{15}.b^{2}.(-2,5).c^{2} \right ].(x^{m}.x^{n}.x^{m-2n}).(y^{n-1}.y^{m-3}.y^{3})$

= $-a^{2}b^{2}c^{2}.x^{2m-n}.y^{n+m-1}$

Câu 2. Tính giá trị của đơn thức $A=\frac{1}{5}x^{3}y^{2}$ và $B=-10xy^{4}$ . Hai đơn thức có thể cùng có giá trị dương được hay không?

Giải:

Xét tích hai đơn thức: $A.B=\frac{1}{5}.x^{5}.y^{2}.(-10xy^{4})=-2x^{4}y^{6}$

Có: $x^{4}\geq  0,\forall x$ và $y^{6}\geq  0,\forall y$ nên $x^{4}y^{6}\geq  0, \forall x,y$

Từ đó suy ra $-2x^{4}y^{6}\leq  0,\forall x,y\Rightarrow A.B\leq  0,\forall x,y$

Vậy hai đơn thức A và B không thể cùng có giá trị dương.

Câu 3: Cho hai đơn thức: $A=2x^{3}$ ;  $B=-xy^{4}$ và $C=-3y^{4}z^{2}$. Chứng minh ba đơn thức không thể cùng có giá trị âm.

Giải:

Xét tích ba đơn thức: $A.B.C=2x^{3}.(-xy^{4}).(-3y^{4}.z^{2})=6x^{4}y^{8}z^{2}$

Có: $x^{4}\geq  0,\forall x$ và $y^{8}\geq  0, \forall y,z^{2}\geq 0\forall z$ nên $x^{4}y^{8}z^{2}\geq 0,\forall x,y$.

Từ đó suy ra $x^{4}y^{8}z^{2}\geq 0,\forall x,y\Rightarrow 0,\forall x,y,z$

Vậy ba đơn thức A, B và C không thể cùng có giá trị âm.

Câu 4. Viết các đơn thức sau thành tổng hoặc hiệu của các đơn thức trong đó có một đơn thức bằng $x^{2}y$

a) $5x^{2}y$                  b)  $-2x^{2}y$                                c) $x^{2}y$

Giải:

a) $5x^{2}y=4x^{2}y +x^{2}y$
b) $-2x^{2}y=x^{2}y-3x^{2}y$
c) $x^{2}y=2x^{2}y-x^{2}y$