Soạn giáo án điện tử Toán 9 KNTT chương 4 Luyện tập chung

Nội dung giáo án

KÍNH CHÀO 

QUÝ THẦY CÔ VÀ CÁC BẠN 

ĐẾN VỚI BUỔI HỌC HÔM NAY

KHỞI ĐỘNG

Một cầu trượt trong công viên có độ dốc là và có độ cao 2,1cm. Tính độ dài của mặt cầu trượt (làm tròn đến chữ số thập phân thứ nhất).

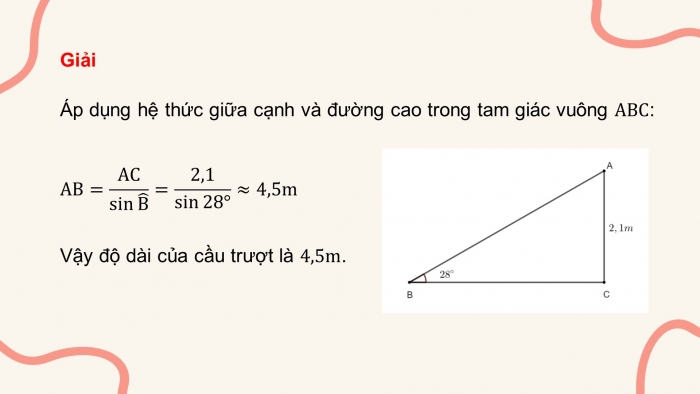
Giải

Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông :

Vậy độ dài của cầu trượt là .

LUYỆN TẬP CHUNG

Hoạt động 1: 

Ôn tập lại kiến thức đã học

1. Nhắc lại kiến thức

Định nghĩa tỉ số lượng giác của một góc nhọn

• Tỉ số giữa cạnh đối và cạnh huyền gọi là sin của kí hiệu .
•  Tỉ số giữa cạnh kề và cạnh huyền gọi là côsin của kí hiệu .
• Tỉ số giữa cạnh đối và cạnh kề gọi là tang của kí hiệu .
•  Tỉ số giữa cạnh kề và cạnh đối gọi là côtang của kí hiệu .

Ví dụ 1.a: SGK – tr.79

Cho tam giác ABC vuông tại A, AB = 5 cm, 

AC = 12 cm.

a) Tính các tỉ số lượng giác của góc B.

Giải

Xét tam giác ABC vuông tại A. Theo định lí Pythagore, ta có

BC² = AB² + AC² = 5² + 12² = 169, suy ra BC = 13 cm

Ta có sinB = = , cosB = =  , tanB = = , cotB = =  

Định lí

Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.

Ví dụ 1.b: SGK – tr.79

Cho tam giác ABC vuông tại A, 

AB = 5 cm, AC = 12 cm.

b) Từ kết quả câu a) suy ra các tỉ số lượng giác của góc C.

Giải

Do + = 90 nên

sinC = cosB = , cosC = sinB =  , tanC = cotB = , cotC = tanB =  

Hệ thức giữa cạnh và góc trong tam giác vuông

• Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề.
• Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh góc vuông kia nhân với tang góc đối hoặc nhân với côtang góc kề.

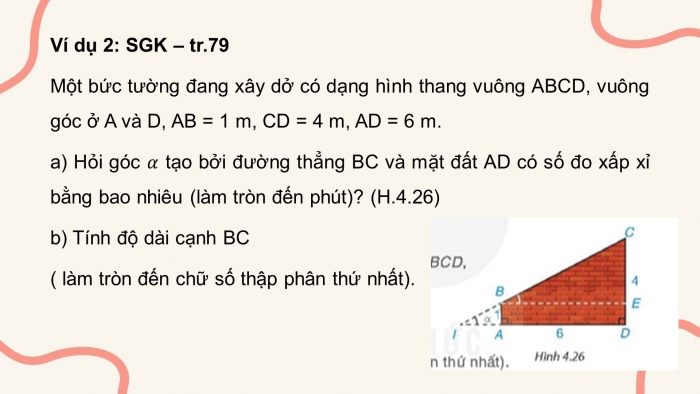
Ví dụ 2: SGK – tr.79

Một bức tường đang xây dở có dạng hình thang vuông ABCD, vuông góc ở A và D, AB = 1 m, CD = 4 m, AD = 6 m.

a) Hỏi góc tạo bởi đường thẳng BC và mặt đất AD có số đo xấp xỉ bằng bao nhiêu (làm tròn đến phút)? (H.4.26)

b) Tính độ dài cạnh BC 

( làm tròn đến chữ số thập phân thứ nhất).

Giải

a) Gọi I là giao điểm của hai đường thẳng AD và BC. Qua B kẻ đường thẳng song song với AD (mặt đất) cắt CD ở E thì khi đó = = (hai góc đồng vị).

Tứ giác ABED có BE // AD, AB // DE, = 90 nên ABED là hình chữ nhật

Do đó BE = AD = 6 m, EC = CD – ED = 4 – 1 = 3 (m).

Xét BCE vuông tại E, ta có tan = tan = = =

Từ đó tính được 2634’

b) Cách 1. Áp dụng định lí Pythagore vào tam giác BEC vuông tại E, ta có:

BC² = BE² + EC² = 6² + 3² = 45. Suy ra BC = = 3 6,7 (m).

Cách 2. Tam giác BEC vuông tại E nên EC = BC . sin ,

Suy ra BC = = 6,7 (m). 

LUYỆN TẬP

CÂU HỎI TRẮC NGHIỆM

Câu 1. Cho tam giác vuông tại có là đường cao, cạnh . Kết luận nào sau đây là đúng ?

A. . 

B. .  

C. . 

D. . 

Câu 2. Cho tam giác vuông tại , có . Khẳng định nào sau đây đúng ? 

…………..

Câu 5. Cho tam giác vuông tại và là đường cao. Cho biết . Khi đó độ dài bằng :

4.14. Một cuốn sách khổ 17 x 24 cm, tức là chiều rộng 17 cm, chiều dài 24 cm. Gọi là góc giữa đường chéo và cạnh 17 cm. Tính sin , cos (làm tròn đến chữ số thập phân thứ hai) và tính số đo (làm tròn đến độ).

Giải

Xét vuông tại , theo định lí Pythagore, ta có :

Theo định nghĩa tỉ số lượng giác, ta có :

,

Suy ra .

4.15. Cho tam giác ABC có chân đường cao AH nằm giữa B và C. Biết HB = 3 cm, HC = 6 cm, = 60. Hãy tính độ dài các cạnh (làm tròn đến cm), số đo các góc của tam giác ABC (làm tròn đến độ).

--------------- Còn tiếp ---------------