Soạn giáo án điện tử Toán 9 KNTT bài 12: Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng

Nội dung giáo án

XIN CHÀO CÁC EM HỌC SINH! CHÀO MỪNG CÁC EM ĐẾN VỚI BÀI HỌC HÔM NAY 

KHỞI ĐỘNG

Để đo chiều cao của một tòa lâu đài (H.4.11), người ta đặt giác kế thẳng đứng tại điểm M. Quay ống ngắm của giác kế sao cho nhìn thấy đỉnh P’ của tòa lâu đài dưới góc nhọn . Sau đó, đặt giác kế thẳng đứng tại điểm N, NM = 20m, thì nhìn thấy đỉnh P’ dưới góc nhọn (). Biết chiều cao giác kế là 1,6m, hãy tính chiều cao của tòa lâu đài.

BÀI 12. MỘT SỐ HỆ THỨC GIỮA CẠNH, GÓC TRONG TAM GIÁC VUÔNG 

VÀ ỨNG DỤNG

NỘI DUNG BÀI HỌC

1. HỆ THỨC GIỮA CẠNH HUYỀN VÀ CẠNH GÓC VUÔNG

HOẠT ĐỘNG 1

                                                Cho tam giác ABC vuông tại A, cạnh huyền a và các cạnh góc vuông b, c (H.4.12)

+ Viết các tỉ số lượng giác sin, côsin của góc và góc theo độ dài các cạnh của tam giác

+ Tính mỗi cạnh góc vuông và theo cạnh huyền và các tỉ số lượng giác trên của góc và góc .

Giải

a)

b) Ta có: 

Tương tự, ta cũng có: 

Định lí 1

Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề.

Chú ý. Trong tam giác vuông tại (H.4.12), ta có: 

Ví dụ 1: SGK – tr.75

Một chiếc máy bay bay lên với vận tốc 500 km/h. Đường bay lên tạo với phương nằm ngang một góc 30 (H.4.13). Hỏi sau 1,2 phút, máy bay lên cao được bao nhiêu kilômét theo phương thẳng đứng? 

Giải

Giả sử trong Hình 4.13, AB là đoạn đường máy bay bay lên trong 1,2 phút thì BH chính là độ cao máy bay đạt được sau 1,2 phút đó.

Ta có 1,2 phút = giờ nên AB = 500 . = 10 (km)

Tam giác ABH vuông tại H, có = 30. Theo Định lí 1, ta có

BH = AB . sinA = 10 . sin30 = 10 . = 5 (km).

Vậy sau 1,2 phút, máy bay lên cao được 5 km. 

Luyện tập 1

1. Một chiếc thang dài 3 m. Cần đặt chân thang cách chân tường một khoảng bằng bao nhiêu mét (làm tròn đến số thập phân thứ hai) để nó tạo được với mặt đất một góc “an toàn” 65 (tức là đảm bảo thang chắc chắn khi sử dụng) (H.4.14)?

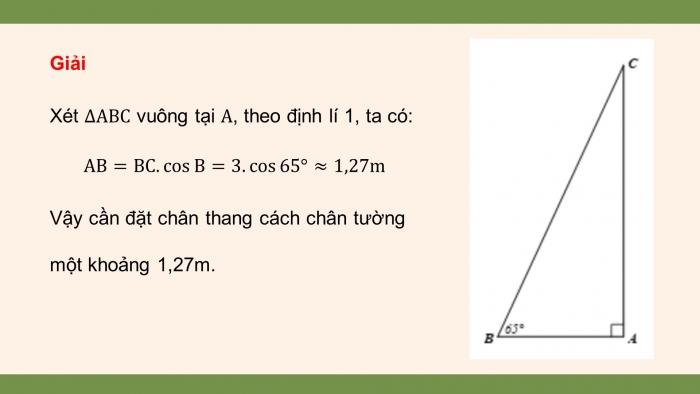
Giải

Xét vuông tại , theo định lí 1, ta có:

Vậy cần đặt chân thang cách chân tường một khoảng 1,27m.

2. Một khúc sông rộng khoảng 250 m. Một con đò chèo qua sông bị dòng nước đẩy xiên nên phải chèo khoảng 320 m mới sang được bờ bên kia. Hỏi dòng nước đã đẩy con đò đi lệch một góc bằng bao nhiêu độ (làm tròn đến phút)? (H.4.15).

Giải

Xét vuông tại , theo định nghĩa tỉ số lượng giác côsin, ta có:

Từ đó tìm được

Vậy dòng nước đã đẩy con đò đi lệch một góc 

2. 

HỆ THỨC GIỮA HAI CẠNH GÓC VUÔNG

HOẠT ĐỘNG 2

Xét tam giác ABC trong Hình 4.16.

a) Viết các tỉ số lượng giác tang, côtang của 

góc và góc theo .

b) Tính mỗi cạnh góc vuông và theo cạnh góc vuông kia và các tỉ số lượng giác trên của góc và góc .

Giải

a)

b) Ta có:

Tương tự:

Định lí 2

Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh góc vuông kia nhân với tang góc đối hoặc nhân với côtang góc kề.

Chú ý. Trong tam giác vuông tại (H.4.16), ta có:

,

.

Ví dụ 2: SGK – tr.76

Các tia nắng mặt trời tạo với mặt đất một góc xấp xỉ bằng 34 và bóng của một toà tháp trên mặt đất dài 8,6 m (H.4.17). Tính chiều cao của toà tháp đó (làm tròn đến mét). 

--------------- Còn tiếp ---------------