Soạn giáo án điện tử toán 10 kết nối bài 20: Vị trí tương đối giữa hai đường thẳng. góc và khoảng cách

Nội dung giáo án

BÀI 20: VỊ TRÍ TƯƠNG ĐỐI GIỮA HAI ĐƯỜNG THẲNG. GÓC VÀ KHOẢNG CÁCH

1. KHỞI ĐỘNG

Vận động viên T chạy trên đường thẳng xuất phát từ A đến B, vận động viên H chạy trên đường thẳng xuất phát từ C đến D (như hình vẽ).

Hỏi trên đường chạy hai vận động viên sẽ chạy qua cùng một vị trí nào?

1. NỘI DUNG BÀI HỌC
2. Vị trí tương đối giữa hai đường thẳng
3. Góc giữa hai đường thẳng
4. Khoảng cách từ một điểm đến một đường thẳng.

III. PHẦN TRIỂN KHAI KIẾN THỨC

1. Vị trí tương đối giữa hai đường thẳng

Em hãy đọc nội dung HĐ1 và trả lời câu hỏi.

HĐ1. Trong mặt phẳng tọa độ, cho hai đường thẳng 

1. a) Điểm M(1; 2) có thuộc cả hai đường thẳng nói trên hay không? 
2. b) Giải hệ 
3. c) Chỉ ra mối quan hệ giữa tọa độ giao điểm của và với nghiệm của hệ phương trình trên. 

Giải:

1. a) Thay vào phương trình đường thẳng ta được:

 (đúng)  

Thay  vào phương trình đường thẳng  ta được:

 (đúng)  

Vậy điểm  thuộc cả hai đường thẳng trên.

1. b)

Vậy hệ phương trình có nghiệm

1. c) Toạ độ giao điểm của và là nghiệm của hệ phương trình trên.

Nhận xét: Mỗi đường thẳng trong mặt phẳng toạ độ là tập hợp những điểm có toạ độ thoả mãn phương trình của đường thẳng đó. Vì vậy, bài toán tìm giao điểm của hai đường thẳng được quy về bài toán giải hệ gồm hai phương trình tương ứng.

Kết luận:

Trên mặt phẳng toạ độ, xét hai đường thẳng:  và

Khi đó toạ độ giao điểm của  và  là nghiệm của hệ phương trình

+  cắt   tại  khi và chỉ khi hệ (*) có nghiệm duy nhất .

+  song song    khi và chỉ khi hệ (*) vô nghiệm.

+  trùng   khi và chỉ khi hệ (*) có vô số nghiệm.

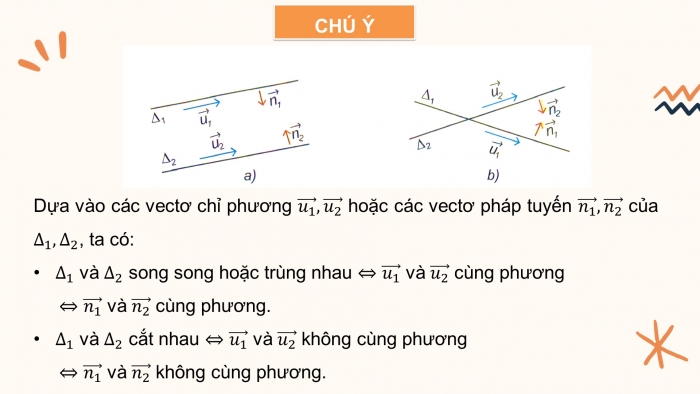
Chú ý:

Hình ảnh

Dựa vào các vectơ chỉ phương  hoặc các vectơ pháp tuyến  của , ta có:

+  và  song song hoặc trùng nhau   và  cùng phương   và  cùng phương.

+  và  cắt nhau   và  không cùng phương   và  không cùng phương.

Em hãy đọc nội dung Ví dụ 1 và trả lời câu hỏi.

Ví dụ 1 (SGK – tr.37)

Xét vị trí tương đối giữa đường thẳng  và mỗi đường thẳng sau:

Giải
Ta có 0

Vậy  và  là một, nói cách khác chúng trùng nhau.
Hai đường thẳng  và  có hai vectơ pháp tuyến  và  cùng phương. Do đó, chúng song song hoặc trùng nhau. Mặt khác, điểm  thuộc đường thẳng  nhưng không thuộc đường thẳng , nên hai đường thẳng này không trùng nhau.
Vậy  và  song song với nhau.

Nhận xét:

Giả sử hai đường thẳng  có hai vectơ chỉ phương  (hay hai vectơ pháp tuyến ) cùng phương. Khi đó:

- Nếu  và  có điểm chung thì  trùng

- Nếu tồn tại điểm thuộc  nhưng không thuộc  thì  song song với .

Em hãy đọc nội dung Luyện tập 1 và trả lời câu hỏi.

Luyện tập 1:

Xét vị trí tương đối giữa các cặp đường thẳng sau: 

1. a) và
2. b) và

Giải:

1. a) Ta có: , do đó hai vectơ pháp tuyến không cùng phương.

Vậy hai đường thẳng  và  cắt nhau.

1. b) Ta có: , do đó hai vectơ pháp tuyến cùng phương và song song hoặc trùng nhau.

Lấy điểm  thuộc  nhưng không thuộc

Vậy hai đường thẳng  và  song song.

2. Góc giữa hai đường thẳng

Em hãy đọc nội dung HĐ2 và trả lời câu hỏi.

HĐ2. Hai đường thẳng  và cắt nhau tạo thành bốn góc (H.7.6). Các số đo của bốn góc đó có mối quan hệ gì với nhau?

Hình ảnh

Giải:

Hai đường thẳng cắt nhau tạo thành 2 cặp góc đối đỉnh bằng nhau.