Soạn giáo án điện tử toán 10 kết nối bài 19: Phương trình đường thẳng (2 tiết)

Nội dung giáo án

CHƯƠNG VII: PHƯƠNG PHÁP TOẠ ĐỘ TRONG MẶT PHẲNG

BÀI 19: PHƯƠNG TRÌNH ĐƯỜNG THẲNG (2 TIẾT)

1. KHỞI ĐỘNG

Một máy bay cất cánh từ sân bay theo một đường thẳng nghiêng với phương nằm ngang một góc , vận tốc cất cánh là . Hình  minh hoạ hình ảnh đường bay của máy bay trên màn hình ra-đa của bộ phận không lưu.

Hãy xác định vị trí của máy bay tại những thời điểm quan trọng (chẳng hạn: 30s, 60s, 90s, 120s).

Hình ảnh

1. NỘI DUNG BÀI HỌC
2. Phương trình tổng quát của đường thẳng
3. Phương trình tham số của đường thẳng.

III. PHẦN TRIỂN KHAI KIẾN THỨC

1. Phương trình tổng quát của đường thẳng

Em hãy đọc nội dung HĐ1 và trả lời câu hỏi.

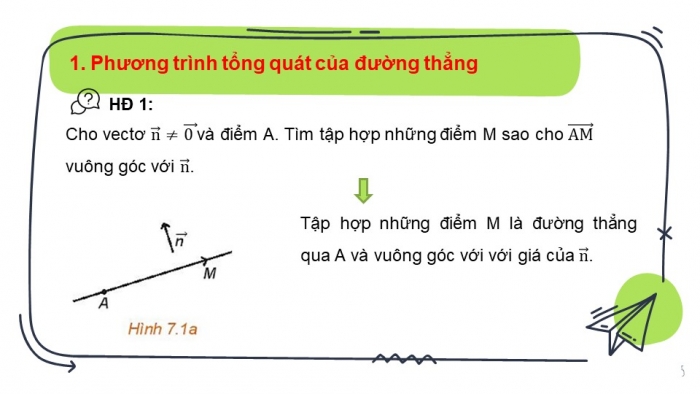
HĐ1. Cho vectơ và điểm A. Tìm tập hợp những điểm M sao cho  vuông góc với .

Tập hợp những điểm M là đường thẳng qua A và vuông góc với với giá của .

Định nghĩa: Vectơ  khác  được gọi là vectơ pháp tuyến của đường thẳng  nếu giá của nó vuông góc với .

Nhận xét:

- Nếu  là vectơ pháp tuyến của đường thẳng  thì  cũng là vectơ pháp tuyến của .

- Đường thẳng hoàn toàn xác định nếu biết một điểm và một vectơ pháp tuyến của nó.

Em hãy đọc nội dung Ví dụ 1 và trả lời câu hỏi.

Ví dụ 1 (SGK – tr.31)

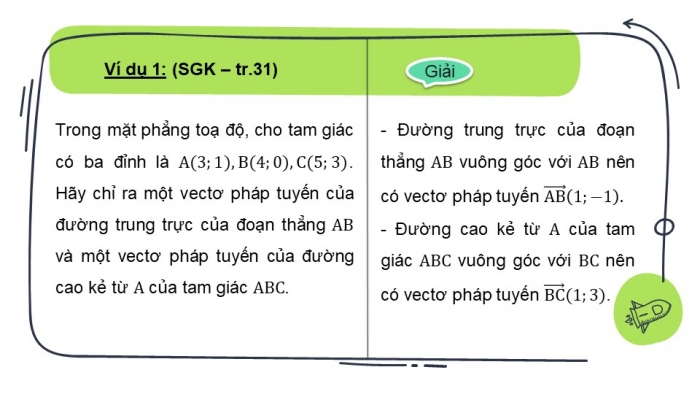
Trong mặt phẳng toạ độ, cho tam giác có ba đỉnh là . Hãy chỉ ra một vectơ pháp tuyến của đường trung trực của đoạn thẳng  và một vectơ pháp tuyến của đường cao kẻ từ  của tam giác .
Giải:
Đường trung trực của đoạn thẳng  vuông góc với  nên có vectơ pháp tuyến .
Đường cao kẻ từ  của tam giác  vuông góc với  nên có vectơ pháp tuyến .

Em hãy đọc nội dung HĐ2 và trả lời câu hỏi.

HĐ2. Trong mặt phẳng toạ độ, cho đường thẳng  đi qua điểm  và có vectơ pháp tưyến . Chứng minh rằng điểm  thuộc  khi và chỉ khi

Giải:

Xét tích

 hay  có giá trùng với đường thẳng .

Nhận xét:

Nếu đặt  thì (1) còn được viết dưới dạng  và được gọi là phương trình tổng quát của  khi và chỉ khi toạ độ của nó thoả mãn phương trình tổng quát của .

Kết luận:

Trong mặt phẳng toạ độ, mọi đường thẳng đều có phương trình tổng quát dạng , với a và b không đồng thời bằng 0. Ngược lại, mỗi phương trình dạng , với a và b không đồng thời bằng 0, đều là phương trình của một đường thẳng, nhận  là một vectơ pháp tuyến.

Em hãy đọc nội dung Ví dụ 2 và trả lời câu hỏi.

Ví dụ 2 (SGK – tr.31)

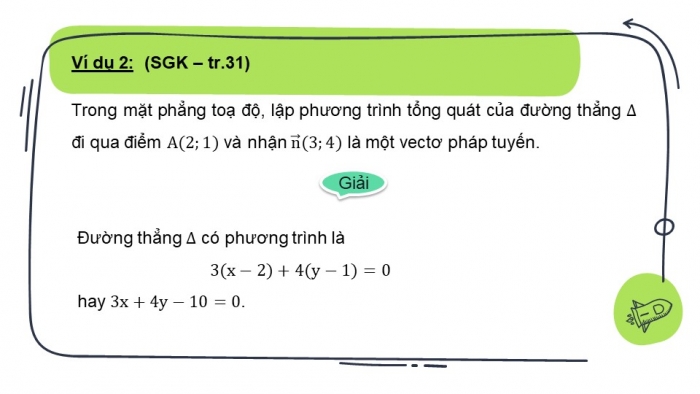
Trong mặt phẳng toạ độ, lập phương trình tổng quát của đường thẳng  đi qua điểm  và nhận  là một vectơ pháp tuyến.
Giải
Đường thẳng  có phương trình là  hay .

Em hãy đọc nội dung Luyện tập 1 và trả lời câu hỏi.

Luyện tập 1:

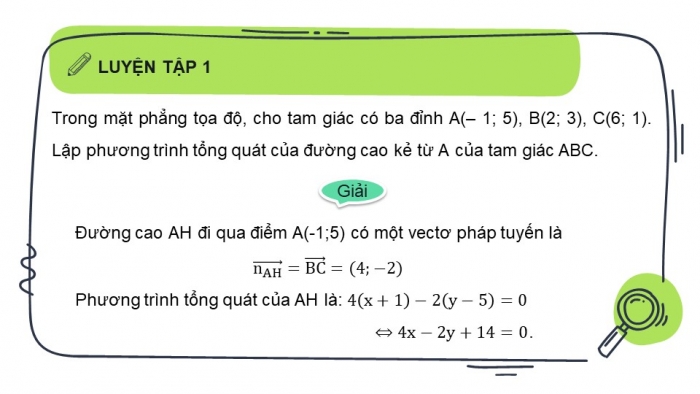
Trong mặt phẳng tọa độ, cho tam giác có ba đỉnh A(– 1; 5), B(2; 3), C(6; 1). Lập phương trình tổng quát của đường cao kẻ từ A của tam giác ABC. 

Giải:

Đường cao AH đi qua điểm A(-1;5) có một vectơ pháp tuyến là .

Phương trình tổng quát của AH là:

.

Em hãy đọc nội dung Ví dụ 3 và trả lời câu hỏi.

Ví dụ 3 (SGK – tr.32)

Trong mặt phẳng toạ độ, lập phương trình đường thẳng  đi qua điểm  và có vectơ pháp tuyến , với  là các số cho trước. Đường thẳng  có mối liên hệ gì với đồ thị của hàm số .
Giải
Đường thẳng  có phương trình là  hay .
Đường thẳng  là tập hợp những điểm  thoả mãn , hay là .
Do đó, đường thẳng  chính là đồ thị của hàm số .

Em hãy đọc nội dung Luyện tập 2 và trả lời câu hỏi.

Luyện tập 2:

Hãy chỉ ra một vectơ pháp tuyến của đường thẳng

Giải:

Ta có:

Một vectơ pháp tuyến của đường thẳng  là .

Nhận xét: Trong mặt phẳng toạ độ, cho đường thẳng

+) Nếu  thì phương trình có thể đưa về dạng  (với ) và  vuông góc với