Giải hoạt động 3 trang 34 chuyên đề toán 10 kết nối tri thức
Hoạt động 3: Tính chất của kCn
a,Quan sát ba dòng đầu, hoàn thành tiếp hai dòng cuối theo mẫu
(a + b)1 = a + b = C01a+C01bC10a+C10b
(a + b)2 = a2 + 2ab + b2 = C02a2+C12ab+C02b2C20a2+C21ab+C20b2
(a + b)3 = a3 + 3a2b + 3ab2 + b3 = C03a3+C13a2b+C23ab2+C03b3C30a3+C31a2b+C32ab2+C30b3
(a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4 = ...
(a + b)5 = a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + b5 = ...
Nhận xét rằng các hệ số khai triển của hai số hạng cách đều số hạng đầu và số hạng cuối luôn bằng nhau. Hãy so sánh, chẳng hạn,
Từ đó hãy dự đoán hệ thức giữa 
b) Dựa vào kết quả của HĐ3a, ta có thể viết những hàng đầu của tam giác Pascal dưới dạng:
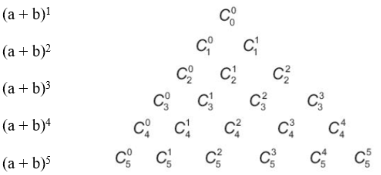
Từ tính chất của tam giác Pascal, hãy so sánh
Từ đó hãy dự đoán hệ thức giữa 
a) (a + b)^4 = a^4 + 4a^3b + 6a^2b^2 + 4ab^3 + b^4
b, Ta thấy 
Dự đoán: 
Xem toàn bộ: Giải chuyên đề toán 10 kết nối bài 4 nhị thức Newton
Giải những bài tập khác
Giải bài tập những môn khác
Giải SGK 10 KNTT
Giải SGK 10 CTST
Giải SGK 10 Cánh diều
Giải SBT lớp 10 kết nối tri thức
Giải SBT lớp 10 chân trời sáng tạo
Giải SBT lớp 10 Cánh diều
Giải chuyên đề học tập 10 Kết nối tri thức
Giải chuyên đề học tập 10 Chân trời sáng tạo
Giải chuyên đề học tập 10 Cánh diều
Trắc nghiệm 10 Kết nối tri thức
Trắc nghiệm 10 Chân trời sáng tạo
Trắc nghiệm 10 Cánh diều
Bình luận