Giải câu 6 bài ba đường conic trong mặt phẳng tọa độ

Chọn hệ tọa độ như hình vẽ:

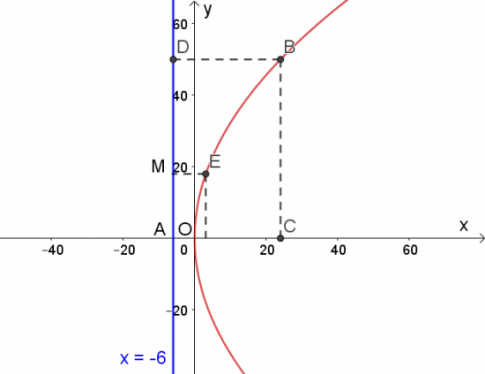
Theo bài ra ta có: AO = 6m, AD = 50 m, BD = 30m $\Rightarrow$ điểm B có tọa độ B(24; 50).

Gọi phương trình của parabol (P) là $y^{2}$ = 2px.

Vì B(24; 50) $\in$ (P) nên thay tọa độ điểm B vào phương trình (P), ta được:

$50^{2}$ = 2p. 24 $\Rightarrow$ p = $\frac{625}{12}$

$\Rightarrow$ Phương trình (P) là: $y^{2}$ = $\frac{625}{6}$x

Ta có: Độ dài đoạn ME chính là chiều dài của thanh cách điểm giữa cầu 18m. Gọi E = (m, 18), vì E $\in$ (P) nên thay tọa độ E vào phương trình P, ta được: $18^{2}$ = $\frac{625}{6}$. m 

$\Rightarrow$ m = 3,1104

$\Rightarrow$ ME = 6 + 3,1104 = 9,1104 (m)

Vậy thanh cáp cách điểm giữa cầu 18m có chiều dài là 9,1104m.