Giải bài tập 9 trang 70 SBT toán 7 tập 2 kết nối
9. Cho đa thức $F(x)=x^{4}-x^{3}-6x^{2}+15x-9$
a)Kiểm tra lại rằng x = 1 và x = -3 là hai nghiệm của F(x).
b)Tìm đa thức G(x) sao cho $F(x)=(x-1)(x-3)\times G(x)$
a) Ta có:
$F(1)=1^{4}-1^{3}-6\times 1^{2}+15\times 1-9=0$
$F(3)=3^{4}-3^{3}-6\times 3^{2}+15\times 3-9$
Vậy x = 1 và x = -3 là hai nghiệm của F(x).
b) $F(x)=(x-1)(x+3)\times G(x)$
=> G(x) = F(x) : [(x - 1)(x + 3)]
=> $G(x) = (x^{4}-x^{3}-6x^{2}+15x-9):(x^{2}+2x-3)$
Ta đặt tính chia:
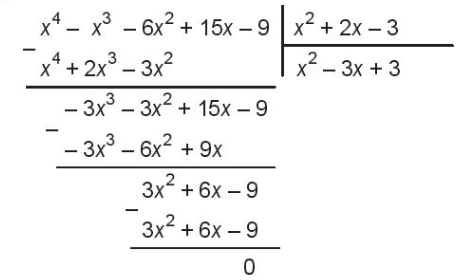
Kết quả ta được $G(x)=x^{2}-3x+3$
Xem toàn bộ: Giải SBT toán 7 Kết nối Bài tập ôn tập cuối năm
Giải những bài tập khác
Giải bài tập những môn khác
Giải sgk lớp 7 cánh diều
Giải SBT lớp 7 kết nối tri thức
Giải SBT lớp 7 chân trời sáng tạo
Giải SBT lớp 7 cánh diều
Trắc nghiệm 7 Kết nối tri thức
Trắc nghiệm 7 Chân trời sáng tạo
Trắc nghiệm 7 Cánh diêu
Bình luận