Giải bài tập 4.7 trang 50 SBT toán 10 tập 1 kết nối

Trả lời:

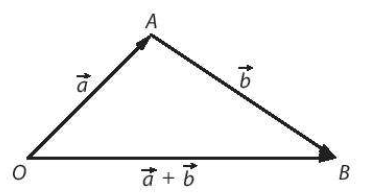
Từ một điểm O t kì, ta vẽ $\overrightarrow{OA}$ = $\overrightarrow{a}$ rồi vẽ $\overrightarrow{AB}$ = $\overrightarrow{b}$.

Khi đó $\overrightarrow{OB} = \overrightarrow{a} + \overrightarrow{b}$ 

Vì $\overrightarrow{a}$, $\overrightarrow{b}$ không cùng phương nên O, A, B không thẳng hàng. Khi đó, trong tam giác OAB, ta có

OA - AB < OB < OA + AB hay là $|\overrightarrow{a}| - |\overrightarrow{b}| < |\overrightarrow{a} + \overrightarrow{b}| < |\overrightarrow{a}| + |\overrightarrow{b}|$