Giải Bài tập 4.24 trang 89 sgk Toán 8 tập 1 Kết nối

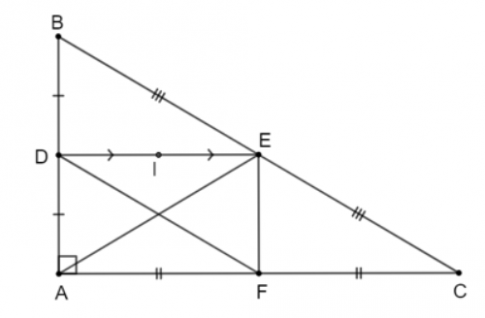
a) D, E, F lần lượt là trung điểm của AB, BC, AC suy ra DE, EF là đường trung bình của tam giác ABC

$\Rightarrow DE//AC, EF//AB$ 

Mà $AB\perp AC\Rightarrow  DE\perp AB, EF\perp AC$

Xét tứ giác ADEF có: $\widehat{ADE}=\widehat{AFE}=\widehat{DAF}=90^{\circ}$ 

Do đó ADEF là hình chữ nhật suy ra AE = DF (2 đường chéo)

b) Xét tứ giác DBEF có: DB// EF, BE // DF suy ra DBEF là hình bình hành 

I là trung điểm của DE nên I cũng là trung điểm của BF 

Vậy ba điểm B, I, F thẳng hàng