Giải Bài tập 3.42 trang 74 sgk Toán 8 tập 1 Kết nối

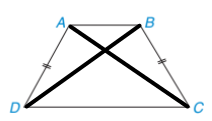
Xét tam giác ABD và BAC ta có:

AB chung

AD = BC (gt)

BD = AC (gt)

Suy ra $\Delta ABD=\Delta BAC$ (c.c.c) $\Rightarrow \widehat{ABD}=\widehat{BAC}$

Xét tam giác ADC và BCD ta có:

AD = BC

DC chung

AC = BD

Suy ra $\Delta ADC=\Delta BCD$ (c.c.c) $\Rightarrow \widehat{ACD}=\widehat{BDC}$

Gọi giao điểm của AC và BD là O

$\widehat{ABD}=\widehat{BAC}$ suy ra tam giác OAB cân tại O $\Rightarrow \widehat{ABD}=\widehat{BAC}=\frac{180^{\circ}-\widehat{AOB}}{2}$

$\widehat{ACD}=\widehat{BDC}$ suy ra tam giác ODC cân tại O $\Rightarrow \widehat{ACD}=\widehat{BDC}=\frac{180^{\circ}-\widehat{DOC}}{2}$

Mà $\widehat{AOB}=\widehat{DOC}$ (đối đỉnh) $\Rightarrow \widehat{ABD}=\widehat{BDC}$ , hai góc này ở vị trí so le trong nên AB // CD, do đó ABCD là hình thang

Xét hình thang ABCD có AC = BD suy ra ABCD là hình thang cân