Giải bài tập 2.9 trang 23 SBT toán 10 tập 1 kết nối
Bài tập 2.9. Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 12 g hương liệu, 9 lít nước và 315 g đường để pha chế hai loại nước A và B. Để pha chế 1 lít nước A cần 45 g đường, 1 lít nước và 0,5 g hương liệu; để pha chế 1 lít nước B cần 15 g đường, 1 lít nước và 2 g hương liệu. Mỗi lít nước A nhận được 60 điểm thưởng, mỗi lít nước B nhận được 80 điểm thưởng. Hỏi cần pha chế bao nhiêu lít nước mỗi loại để đội chơi được số điểm thưởng là cao nhất?
Trả lời:
Gọi số lít nước A và B cần pha chế lần lượt là x lít và y lít (x ≥ 0; y ≥ 0).
Do 1 lít nước A cần 45 g đường, 1 lít nước và 0,5 g hương liệu nên x lít nước A cần 45x g đường, x lít nước và 0,5x g hương liệu.
Do 1 lít nước B cần 15 g đường, 1 lít nước và 2 g hương liệu nên y lít nước A cần 15y g đường, y lít nước và 2y g hương liệu.
Do có tối đa 12g hương liệu, 9 lít nước và 315 g đường nên 45x + 15y ≤ 315; x + y ≤ 9 và 0,5x + 2y ≤ 12.
Khi đó ta có hệ bất phương trình 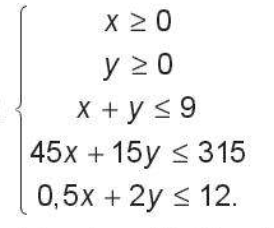
Số điểm thưởng đội chơi nhận được là F(x; y) = 60x + 80y (điểm). Ta cần tìm giá trị lớn nhật của F(x; y) với (x; y) thoả mãn hệ trên.
Miền nghiệm của hệ là miền ngũ giác OABCD với A(0; 6), B(4; 5), C(6; 3), D(7: 0) và O(0; 0).


Bình luận