Giải bài tập 2 trang 104 sgk Toán 8 tập 1 CD

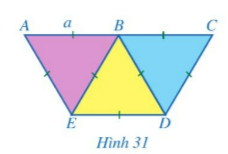
a. Vì 3 tam giác ABE, BED, BDC là các tam giác đều có cạnh bằng nhau nên:

$\widehat{ABE}$ = $\widehat{DBE}$ => AB//ED

$\widehat{CBD}$ = $\widehat{EBD}$ => BC//ED

Như vậy AB và BC cùng // với ED lại có chung điểm B nên 3 điểm A, B, C thẳng hàng.(đpcm)

b. Xét tứ giác ACDE có: 

AC // DE=> tứ giác ACDE là hình thang

2 cạnh bên AE = CD (đều = a)

=> ACDE là hình thang cân. 

c. Diện tích của tứ giác ACDE = Tổng diện tích của 3 tam giác ABE, BED, BDC mà 3 tam giác ABE, BED, BDC đều bằng nhau nên ta chỉ cần tính diện tích của một tam giác BED. 

Gọi BM là đường cao của tam giác BED. Khi đó BM = $\sqrt{a^{2}-\left ( \frac{a}{2} \right )^{2}}=\frac{a\sqrt{3}}{2}$

Diện tích tam giác BED là: $\frac{1}{2}.BM.ED = \frac{1}{2}.\frac{a\sqrt{3}}{2}.a=\frac{a^{2}\sqrt{3}}{4}$

=> Diện tích của tứ giác ACDE = 3. $\frac{a^{2}\sqrt{3}}{4}$ = $\frac{a^{2}\sqrt{3}.3}{4}$