Giải bài tập 13 trang 121 sgk Toán 8 tập 1 CD

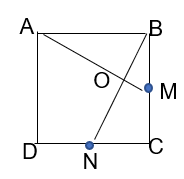
a. Xét 2 tam giác vuông:  $\Delta ABM$ và  $\Delta BCN$ có: 

• AB = BC (2 cạnh của hình vuông ABCD)
• BM = NC (M, N là trung điểm của mỗi cạnh hình vuông)

=> $\Delta ABM$ =  $\Delta BCN$ (2 cạnh gọc vuông)

b. Từ a suy ra: $\widehat{BAM}=\widehat{CBN}$ hay $\widehat{BAO}=\widehat{MBO}$

c. Xét tam giác ABM có: 

$\widehat{BAO}+\widehat{BMO}$ = $90^{\circ}$

kết hợp với b suy ra $\widehat{MBO}+\widehat{BMO}$ = $90^{\circ}$. 

vậy trong tam giác BOM có: $\widehat{BOM} = $180^{\circ} - ($\widehat{MBO}+\widehat{BMO}$) = $180^{\circ} - 90^{\circ}$ = $90^{\circ}$

=> $AM\perp BN$