Giải bài tập 12 trang 121 sgk Toán 8 tập 1 CD
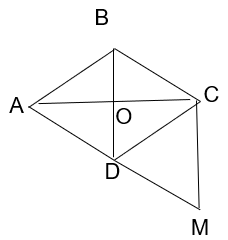
Bài tập 12 trang 121 sgk Toán 8 tập 1 CD: Cho hình thoi ABCD và hình bình hành BCMD. Gọi O là giao điểm của AC và BD.
Chứng minh:
a) OD = $\frac{1}{2}$CM và tam giác ACM là tam giác vuông;
b) Ba điểm A, D, M thẳng hàng;
c) Tam giác DCM là tam giác cân.
a. O là giao điểm của 2 đường chéo hình thoi nên O sẽ là trung điểm của mỗi đường chéo. Vậy OB = OD = $\frac{1}{2}$ BD.
mặt khác, BCMD là hình bình hành nên:
- 2 cạnh đối BD = CM => OD = $\frac{1}{2}$CM
- BD //CM mà AC $\perp $ DB => AC $\perp $ CM => tam giác ACM là tam giác vuông tại C
c. Ta có ABCD là hình thoi nên cạnh BC = AD = DC.
BCMD là hình bình hành nên 2 cạnh đối BC = DM
=> DM = DC. Vậy tam giác DCM là tam giác cân tại D
Xem toàn bộ: Giải toán 8 cánh diều bài Bài tập cuối chương V

Bình luận