Giải bài tập 11 trang 121 sgk Toán 8 tập 1 CD
Bài tập 11 trang 121 sgk Toán 8 tập 1 CD: Cho hình bình hành ABCD. Gọi M là điểm nằm giữa A và B, N là điểm nằm giữa C và D sao cho AM = CN. Gọi I là giao điểm của MN và AC. Chứng minh:
a) $\Delta IAM = \Delta ICN$
b) Tứ giác AMCN là hình bình hành.
c) Ba điểm B, I, D thẳng hàng.
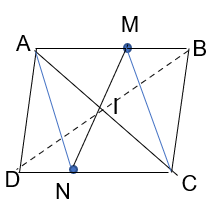
a. ABCD là hình bình hành nên AB//CD. => $\widehat{MAI}=\widehat{NCI}; \widehat{AMI}=\widehat{CNI}$ (2 góc so le trong).
Lại có AM = CN
Vậy $\Delta IAM = \Delta ICN$ (g-c-g)
b. Tứ giác AMCN có AM//NC và AM = NC. Dựa vào dâu hiệu nhận biết tứ giác có 2 cạnh song song và bằng nhau thì tứ giác đó là hình bình hành (đpcm)
Xem toàn bộ: Giải toán 8 cánh diều bài Bài tập cuối chương V
Giải những bài tập khác
Giải bài tập những môn khác
Giải sgk lớp 8 cánh diều
Giải SBT lớp 8 kết nối tri thức
Giải SBT lớp 8 chân trời sáng tạo
Soạn SBT lớp 8 cánh diều
Trắc nghiệm 8 Kết nối tri thức
Trắc nghiệm 8 Chân trời sáng tạo
Trắc nghiệm 8 Cánh diều
Bộ đề thi, đề kiểm tra lớp 8 chân trời sáng tạo
Giáo án lớp 8
Bình luận