Cho tam giác ABC cân tại A và cho $\widehat{A}=124^{\circ}$.
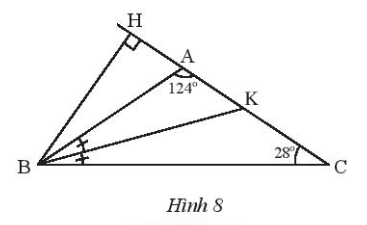
Bài 8. Cho tam giác ABC cân tại A và cho $\widehat{A}=124^{\circ}$. Vẽ đường cao BH và phân giác BK ứng với đỉnh B của tam giác ABC. Tính số đo các góc của tam giác BHK.
Trong tam giác ABC ta có: $\widehat{B}=\widehat{C}=\frac{180^{\circ}-\widehat{A}}{2}=\frac{180^{\circ}-124^{\circ}}{2}=28^{\circ}$
Ta có $\widehat{HKB}=\widehat{AKB}=180^{\circ}-124^{\circ}-14^{\circ}=42^{\circ}$
Trong tam giác vuông BHK ta có $\widehat{BHK}=90^{\circ}; \widehat{HBK}=90^{\circ}-42^{\circ}=48^{\circ}$
Xem toàn bộ: Giải SBT toán 7 Chân trời Bài tập cuối chương 8

Bình luận