Bài tập file word mức độ vận dụng cao bài 14: Hình thoi và hình vuông
4. VẬN DỤNG CAO (3 câu)
Câu 1: Một viên gạch trang trí có dạng hình thoi với độ dài cạnh là 40 cm và số đo một góc là 60° (Hình 63). Diện tích của viên gạch đó là bao nhiêu centimét vuông (làm tròn kết quả đến hàng phần trăm)?

Câu 2. Cho hai mảnh giấy, mỗi mảnh có đạng hình vuông với độ dài cạnh là 1 dm. Hãy trình bày cách cắt phép hai mảnh giấy đó để được một hình vuông có độ dài cạnh là $\sqrt{2}$ dm.
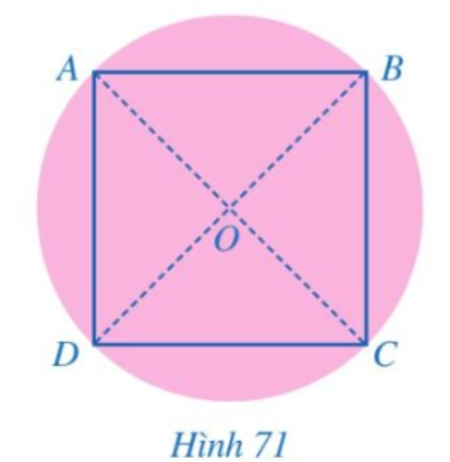
Câu 3. Bạn Thảo có một mảnh giấy có dạng hình tròn. Bạn Thảo đố bạn Minh: Không dùng thước thẳng và compa, làm thế nào có thể xác định tâm của hình tròn và chọn ra 4 vị trí trên đường tròn đó để chúng là 4 đỉnh của một hình vuông? Bạn Minh đã làm như sau:
Bước 1. Gấp mảnh giấy sao cho hai nửa hình tròn trùng khít nhau. Nét gấp thẳng tạo thành đường kính của hình tròn. Ta đánh dấu hai đầu mút của đường kính đó là hai điểm A, C.
Bước 2. Tiếp tục gấp mảnh giấy (có dạng nửa hình tròn) ở Bước 1 sao cho hai nửa mới của nửa hình tròn đó lại trùng khít nhau. Trải miếng bìa về dạng hình tròn ban đầu, ta được nét gấp mới là một đường kính khác của hình tròn.
Bước 3. Ta đánh dấu giao điểm của hai đường kính là O và hai đầu mút của đường kính mới là hai điểm B, D. Khi đó O là tâm của hình tròn và tứ giác ABCD là hình vuông (Hình 7).
Em hãy giải thích cách làm của bạn Minh.
Câu 1:
Tam giác ABC có AB = BC (2 cạnh của hình thoi) nên là tam giác cân tại B. Lại có góc B = 60∘ nên ABC là tam giác đều => AC = 40cm.
Gọi O là giao điểm của 2 đường chéo AC và BD. Khi đó: OA = 12AC = 20cm.
Trong tam giác AOB có:
$\sqrt{AB^{2}-OA^{2}}=\sqrt{40^{2}-20^{2}}=34,6$
Diện tích tam giác $ABC=\frac{1}{2}.OB.AC=\frac{1}{2}.34,6.40=692$ cm2
=> Diện tích viên gạch có dạng hình thoi như trên sẽ là: 2. 692 = 1 384cm2
Câu 2.
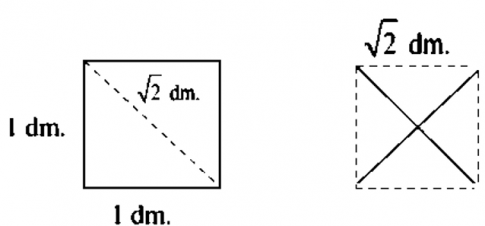
Cách làm:
- Gấp đôi mỗi mảnh giấy có dạng hình vuông theo đường kẻ chéo như hình đầu tiên, đường kẻ này sẽ có độ dài là $\sqrt{2}$ dm (đúng với định lý pythagore). Sau đó dùng kéo cắt theo đường kẻ này ta sẽ có 4 mảnh giấy hình tam giác như nhau.
- Xếp 4 mảnh giấy tam giác này lại sao cho đường cắt của 4 mảnh tạo thành 4 cạnh của hình vuông mới, lúc này cạnh của hình vuông mới sẽ là $\sqrt{2}$ dm
Câu 3.
Giải:
- Giao điểm của 2 đường kính của hình tròn sẽ cách tất cả các điểm trên đường tròn những khoảng cách như nhau gọi là bán kính. Và giao điểm O này chính là tâm của đường tròn.
- Với việc xác định các điểm mút như trên ta đi xét các tam giác sau:
Tam giác AOD và COB có:
OA = OB; OD = OC (đều là bán kính đường tròn)
Góc AOD và BOC bằng nhau (2 góc đối đỉnh)
=> Tam giác AOD và COB bằng nhau (c-g-c). Suy ra:
AD = BC (1)
$\widehat{OAD}=\widehat{OCB}$
=> AD//BC (2)
Tương tự vói 2 tam giác DOC và BOA. Suy ra:
AB = DC. (3)
$\widehat{ODC}=\widehat{OBA}$
=> AB//DC (4)
Từ (2) và (4) => ABCD là hình bình hành. Kết hợp với (1) và (2)
=> ABCD là hình vuông (hình bình hành có 2 cạnh đối song song và bằng nhau)

Bình luận