Bài tập file word mức độ thông hiểu bài 14: Hình thoi và hình vuông
2. THÔNG HIỂU (4 câu)
Câu 1. Cho hình thoi MNPQ có I là giao điểm của hai đường chéo.
a) Tính MP khi biết MN = 10 dm, IN = 6 dm
b) Tính $\widehat{IMN}$ khi biết $\widehat{MNP}=128^{\circ}$
Câu 2. Cho hình 21. Chứng minh rằng tứ giác EFGH là hình thoi.

Câu 3: Cho tam giác ABC cân tại A, gọi M là trung điểm của BC. Lấy điểm D đối xứng với điểm A qua BC.
a) Chứng minh tứ giác ABCD là hình thoi.
b) Gọi E, F lần lượt là trung điểm của AB và AC, lấy điểm O sao cho E là trung điểm của OM. Chứng minh hai tam giác AOB và MBO vuông và bằng nhau
b) Chứng minh tứ giác AEMF là hình thoi.
Câu 4: Cho tam giác ABC vuông tại A có đường phân giác AD. Gọi H, K lần lượt là hình chiếu của D trên AB, AC. Chứng minh tứ giác AHDK là hình vuông.
Câu 1.
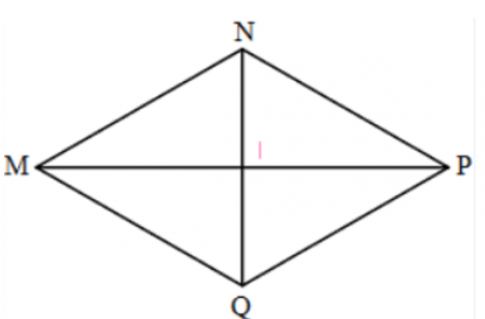
Áp dụng định lí Pythagore cho tam giác MNI vuông tại I:
$MN^{2}=NI^{2}+MI^{2}$ suy ra $MI^{2}=MN^{2}+NI^{2}=10^{2}-6^{2}=64$ do đó MI = 8 dm
b) Ta có: $\widehat{NMQ}=180^{\circ}-128^{\circ}=52^{\circ}$
Lại có MP là phân giác góc $\widehat{NMQ}$ suy ra $\widehat{IMN}=52^{\circ}:2=26^{\circ}$
Câu 2.
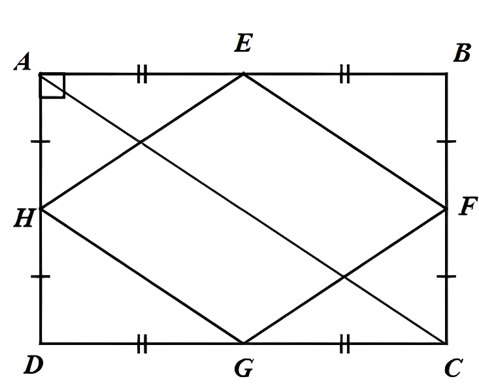
E, F lần lượt là trung điểm của AB và BC
⇒EF là đường trung bình của tam giác ABC
⇒EF//AC và $EF=\frac{1}{2}AC$ (1)
H, G lần lượt là trung điểm của AD và DC
⇒HG là đường trung bình của tam giác ACD
⇒HG//ACvà $HG=\frac{1}{2}AC$ (2)
Từ (1) và (2) ⇒EF//HGvà EF=HG
Vậy tứ giác EFGH là hình bình hành.
Tứ giác ABCD có AB=CDvà AD=BC⇒ Tứ giác ABCD là hình bình hành.
Mà $\widehat{BAD}=90^{\circ}$ ⇒ ABCD là hình chữ nhật.
Xét ΔEBFvà ΔCGFcó :
EB=EC(gt)
BF=FC(gt)
$\widehat{EBF}=\widehat{GCF}(=90^{\circ})$
⇒ΔEBF=ΔGCF(c.g.c)⇒EF=GF
Chứng minh tương tự ta có GF=GH,GH=EF⇒EF=GF=GH=EH
Do đó tứ giác EFGH là hình thoi.
Câu 3:
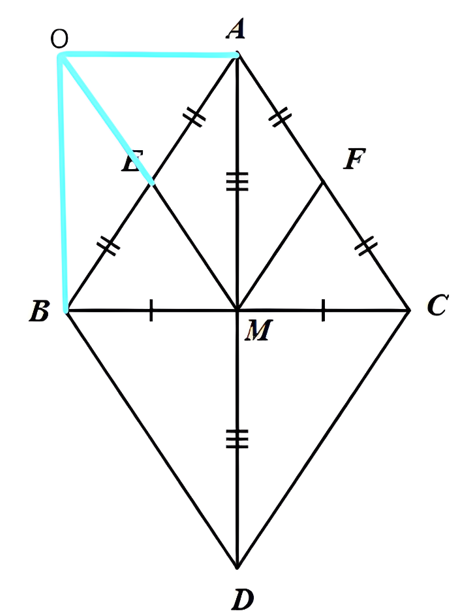
a) Tứ giác ABCD có:
AD và BC cắt nhau tại M (gt);
M là trung điểm của BC (gt)
M là trung điểm của AD (D đối xứng với A qua BC)
Do đó tứ giác ABDC là hình bình hành
Mà AD⊥BC (vì D đối xứng với A qua BC)
Nên hình bình hành ABDC là hình thoi.
b) Tứ giác OAMB có:
OM và AB cắt nhau tại E (gt);
E là trung điểm của OM (gt)
E là trung điểm của AB (gt)
Do đó tứ giác OAMB là hình bình hành
Suy ra $\widehat{AOB}=\widehat{AMB}=90^{\circ}, \widehat{OBM}=\widehat{OAM}=180^{\circ}-90^{\circ}=90^{\circ}$
Do đó AOB và MBO là tam giác vuông.
Xét tam giác AOB và MBO ta có:
AO = MB (OAMB là hình bình hành)
$\widehat{AOB}=\widehat{MBO}=90^{\circ}$
OB chung
Suy ra ΔAOB=ΔMBO (c.g.c)
c) Ta có $ME=\frac{1}{2}AB$ (đường trung tuyến ứng với cạnh huyền)
Và $AE=\frac{1}{2}AB$ (E là trung điểm của AB)
⇒ $EM=EA=\frac{1}{2}AB$ (1)
Ta có $MF=\frac{1}{2}AC$ (đường trung tuyến ứng với cạnh huyền)
Và $AF=\frac{1}{2}AC$ (F là trung điểm của AC)
⇒ $\Rightarrow MF=AF=\frac{1}{2}AC$ (2)
AB=AC (ΔABCcân tại A) (3)
Từ (1), (2) và (3) suy ra EM = EA = MF = AF
Do đó tứ giác AEMF là hình thoi.
Câu 4:
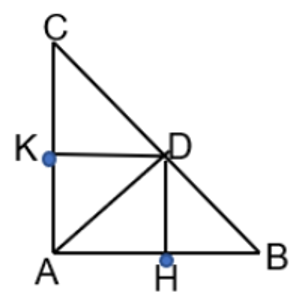
H, K lần lượt là hình chiếu của D trên AB, AC nên $\widehat{DHA}=\widehat{DKA}=90^{\circ}$. Tứ giác AHDK có 3 góc vuông nên góc còn lại cũng là góc vuông. Vậy AHDK là hình chữ nhật.
Xét 2 tam giác vuông DHA và DKA có:
$\widehat{DHA}=\widehat{DKA}$ (AD là đường phân giác của góc A)
AD chung
=> 2 tam giác vuông DHA và DKA bằng nhau theo trường hợp cạnh huyền, góc nhọn
=> 2 cạnh tương ứng AH = AK. Hình chữ nhật AHDK có 2 cạnh liền kề bằng nhau nên là hình vuông (đpcm)

Bình luận