Bài tập file word mức độ nhận biết bài 14: Hình thoi và hình vuông
1. NHẬN BIẾT (5 câu)
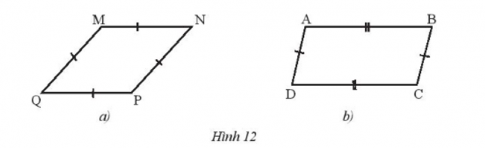
Câu 1: Trong tứ giác ở hình 12, tứ giác nào là hình thoi?
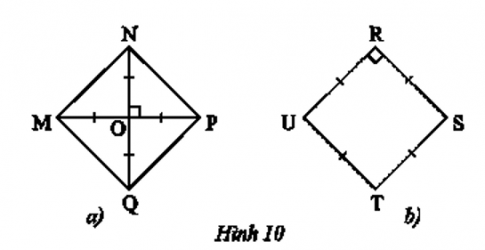
Câu 2: Tìm hình vuông trong hai hình sau
Câu 3: Cho biết các góc và các cạnh của tứ giác ABCD ở Hình 65 có đặc điểm gì.

Câu 4:
a) Mỗi hình vuông có là một hình chữ nhật hay không?
b) Mỗi hình vuông có là một hình thoi hay không?
Câu 5. Cho hình thoi ABCD có AC = BD. Chứng minh ABCD là hình vuông.
Câu 1:
- Tứ giác MNPQ có bốn cạnh bằng nhau nên là hình thoi.
- Tứ giác ABCD chỉ có các cạnh đối bằng nhau nên chỉ là hình bình hành và không phải là hình thoi.
Câu 2:
Xét tứ giác MNPQ có: MP và NQ cắt nhau tại trung điểm của mỗi đường , suy ra MNPQ là hình bình hành. Ta lại có MP vông góc với NQ nên MNPQ là hình thoi suy ra AB = BC = CD = AD (1)
Mặt khác, NO là đường trung tuyến ứng với cạnh MP, $NO=\frac{1}{2}MP$ nên tam giác MNP vuông tại N hay $\widehat{MNP}=90^{\circ}$
Tương tự ta có: $\widehat{NPQ}=\widehat{MQP}=\widehat{NMQ}=\widehat{MNP}=90^{\circ}$ (2)
Từ (1)(2) suy ra MNPQ là hình vuông
Xét tứ giác URST có: UR = RS = ST = UT, $\widehat{URS}=90^{\circ}$ suy ra URST là hình vuông
Câu 3:
Tứ giác ABCD ở Hình 65 có đặc điểm:
- Các góc đều là góc vuông
- Các cạnh đều bằng nhau.
Câu 4:
a) Mỗi hình vuông là một hình chữ nhật.
b) Mỗi hình vuông có là một hình thoi.
Câu 5.
ABCD là hình thoi nên:
- Có các góc đối bằng nhau. Suy ra:
$\widehat{C}=\widehat{A}=90^{\circ}$
$\widehat{B}=\widehat{D}=12(360^{\circ}-\widehat{C}-\widehat{A})$
$=12(360^{\circ}-90^{\circ}-90^{\circ})=90^{\circ}$
- 4 cạnh bằng nhau.
=> ABCD có 4 góc vuông và 4 cạnh bằng nhau nên là hình vuông.(đpcm)

Bình luận