Câu hỏi tự luận mức độ vận dụng Toán 9 cd bài 2: Từ giác nội tiếp đường tròn

Câu 1: 

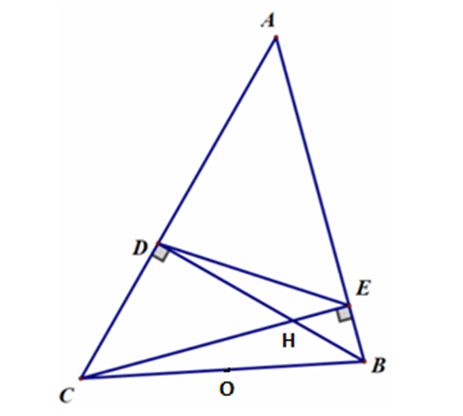
a) Chứng minh là tứ giác nội tiếp.

Vì là các đường cao của nên .

Xét tứ giác có .

là tứ giác nội tiếp (Tứ giác có tổng 2 góc đối bằng ).

b) Chứng minh là tứ giác nội tiếp.

Gọi  là trung điểm.

Vì là các đường cao của nên

Xét tam giác có và là đường trung tuyến nên 

Xét tam giác có và là đường trung tuyến nên

Từ và suy ra

Vậy tứ giác nội tiếp được đường tròn có tâm là trung điểm.

Câu 2: 

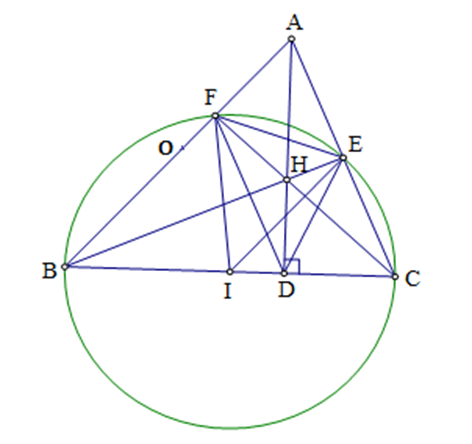
a) Chứng minh tứ giác nội tiếp.

- Xét đường tròn

     (góc nội tiếp chắn nửa đường tròn)

     (góc nội tiếp chắn nửa đường tròn)

- Xét tứ giác

     (chứng minh trên)

tứ giác có tổng hai góc đối bằng nên tứ giác nội tiếp.

b)  Chứng minh tứ giác nội tiếp.

Gọi  là trung điểm.

Xét tam giác có và là đường trung tuyến nên  

Xét tam giác có và là đường trung tuyến nên

Từ và suy ra

Vậy tứ giác nội tiếp được đường tròn có tâm là trung điểm.

Câu 3: 

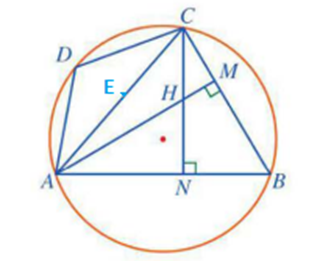
a) Chứng minh .

Vì là các đường cao của nên .

Xét tứ giác có .

là tứ giác nội tiếp (Tứ giác có tổng 2 góc đối bằng ).

Tứ giác nội tiếp nên: hay

mà (hai góc kề bù)

do đó

b) Chứng minh .

Tứ giác nội tiếp nên:  

mà (đối đỉnh)

nên

hay

Mặc khác tứ giác nội tiếp đường tròn tâm nên

Do đó

c) Chứng minh .

Ta chứng minh là tứ giác nội tiếp.

Gọi  là trung điểm.

Xét tam giác có và là đường trung tuyến nên  

Xét tam giác có và là đường trung tuyến nên

Từ và suy ra

Vậy tứ giác nội tiếp được đường tròn có tâm là trung điểm.

Suy ra (góc nội tiếp cùng chắn cung của đường tròn tâm )

d) Chứng minh .

Ta có (hai góc phụ nhau)

Hay

Mà ( tứ giác nội tiếp được đường tròn, câu c))

Nên

Suy ra

Câu 4: 

Ta có . Nếu thì tứ giác nội tiếp. Vì vậy thay vì trực tiếp chỉ ra góc ta sẽ đi chứng minh tứ giác nội tiếp. Tức là ta chứng minh .   

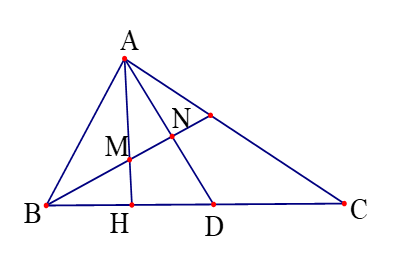
Thật vậy ta có , mà và do cùng phụ với góc từ đó suy ra hay tứ giác nội tiếp

Câu 5:

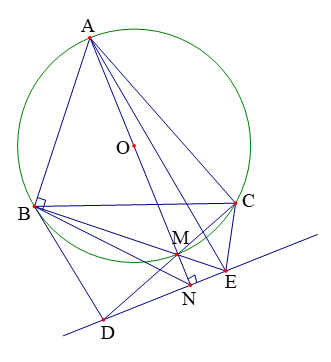
Kẻ đường kính cắt tại .

Ta có nên tứ giác nội tiếp, suy ra .

Mặt khác , do đó hay .

Tứ giác có các đỉnh và cùng nhìn đoạn thẳng dưới một góc không đổi. Vì vậy tứ giác nội tiếp.

Vậy cùng thuộc một đường tròn.

Câu 6: 

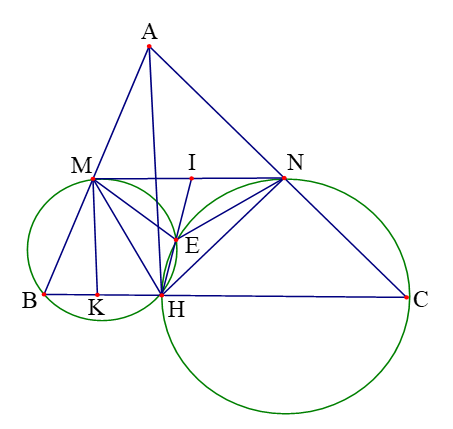
Để chứng minh là tứ giác nội tiếp ta sẽ 

chứng minh: . 

Ta cần tìm sự liên hệ của các góc với các góc có sẵn của những tứ giác nội tiếp khác.

Ta có suy ra . Hay tứ giác là tứ giác nội tiếp.

Kẻ , giả sử cắt tại thì là cát tuyến của hai đường tròn , .

Lại có (Tính chất trung tuyến tam giác vuông). 

Suy ra tam giác cân tại luôn đi qua tâm đường tròn ngoại tiếp tam giác . Hay là tiếp tuyến của suy ra , tương tự ta cũng có là tiếp tuyến của suy ra do đó .

Câu 7: 

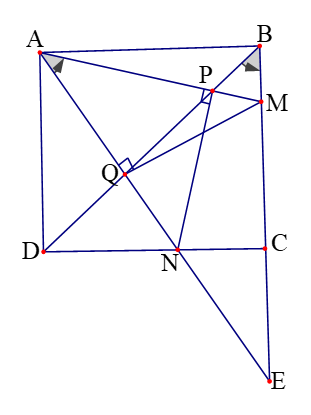
a). Gọi là giao điểm của và .

Các điểm và nằm trên hai cạnh và của tam giác , nên tứ giác là lồi. Các đỉnh và cùng nhìn đoạn thẳng dưới một góc không đổi. Vì vậy tứ giác nội tiếp. 

Lập luận tương tự ta suy ra tứ giác nội tiếp.

b) Từ kết quả câu a, suy ra . Tập hợp các điểm nhìn đoạn dưới một góc vuông, nên các điểm này nằm trên đường tròn đường kính .