Câu hỏi tự luận mức độ vận dụng Toán 9 cd bài 2: Phương trình bậc hai một ẩn
3. VẬN DỤNG (7 câu)
Câu 1: Cho phương trình ![]() (m là tham số). Tìm các giá trị của m để phương trình:
(m là tham số). Tìm các giá trị của m để phương trình:
a) Có hai nghiệm phân biệt
b) Có nghiệm kép
c) Vô nghiệm
d) Có đúng một nghiệm
e) Có nghiệm
Câu 2: Trong mặt phẳng tọa độ ![]() , cho hàm số
, cho hàm số ![]() có đồ thị
có đồ thị ![]() và đường thẳng
và đường thẳng ![]()
a) Vẽ đồ thị ![]() và
và ![]() trên cùng mặt phẳng tọa độ.
trên cùng mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm của ![]() và
và ![]() bằng phép tính.
bằng phép tính.
Câu 3: Trong mặt phẳng tọa độ ![]() cho parabol
cho parabol ![]()
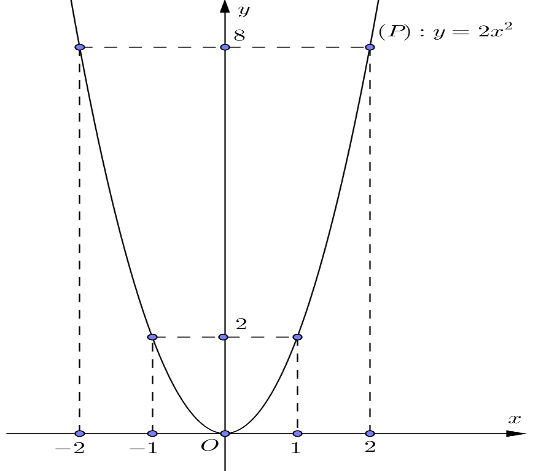
a) Vẽ đồ thị parabol ![]()
b) Bằng phép tính, tìm tất cả các điểm thuộc parabol ![]() (khác gốc tọa độ
(khác gốc tọa độ ![]() ) có tung độ gấp hai lần hoành độ.
) có tung độ gấp hai lần hoành độ.
Câu 4: Cho hàm số ![]() . Với giá trị nào của m thì đồ thị hàm số
. Với giá trị nào của m thì đồ thị hàm số ![]() cắt đường thẳng
cắt đường thẳng ![]() tại điểm có tung độ bằng 2?
tại điểm có tung độ bằng 2?
Câu 5: Cho hàm số ![]() có đồ thị là
có đồ thị là ![]() .
.
a) Vẽ đồ thị ![]() trên mặt phẳng tọa độ.
trên mặt phẳng tọa độ.
b) Tìm ![]() để
để ![]() tiếp xúc với Parabol
tiếp xúc với Parabol ![]() .
.
Câu 6: Cho Parabol ![]() và đường thẳng
và đường thẳng ![]() (
( ![]() là tham số). Tim điều kiện của tham số
là tham số). Tim điều kiện của tham số ![]() đề
đề ![]() cắt
cắt ![]() tại hai điểm nằm về hai phia của trục tung.
tại hai điểm nằm về hai phia của trục tung.
Câu 7: Cho đường thẳng ![]() và Parabol
và Parabol ![]()
a) Tìm m để đường thẳng ![]() đi qua
đi qua ![]()
b) Tìm m để đường thẳng ![]() tiếp xúc với Parabol
tiếp xúc với Parabol ![]()
Câu 1:
Ta có: ![]()
a) Phương tình có hai nghiệm phân biệt khi ![]() và
và ![]() hay
hay ![]() và
và ![]()
b) Xét ![]() Phương trình có nghiệm kép khi
Phương trình có nghiệm kép khi ![]() và
và ![]() hay
hay ![]()
c) Ta tìm được ![]()
d) Ta tìm được ![]()
e) Ta tìm được ![]()
Câu 2:
Lập bảng:
Đường thẳng ![]()
x | 0 | 4 |
| 2 | 0 |
Parabol ![]()
x | -2 | -1 | 0 | 1 | 2 |
| 1 |
| 0 |
| 1 |
Vẽ đồ thị:

b) Tìm tọa độ giao điểm của ![]() và
và ![]() bằng phép tính.
bằng phép tính.
Hoành độ giao điểm của ![]() và
và ![]() là nghiệm của phương trình
là nghiệm của phương trình
![]()
![]()
![]()
Do ![]() nên phương trình đã cho có hai nghiệm phân biệt là
nên phương trình đã cho có hai nghiệm phân biệt là
![]() và
và ![]()
+ Với ![]()
+ Với ![]() .
.
Vậy tọa độ giao điểm của ![]() và
và ![]() là
là ![]() và
và ![]() .
.
Câu 3:
a) Vẽ đồ thị parabol ![]()
Bảng giá trị:
|
|
|
|
|
|
|
|
|
|
|
|
Đồ thị:
b) Gọi ![]() là điểm cần tìm với
là điểm cần tìm với ![]() .
.
Vì ![]() có tung độ gấp hai lần hoành độ nên
có tung độ gấp hai lần hoành độ nên ![]()
Khi đó: ![]()
Vì ![]() nên:
nên:
![]()
![]()
![]()
![]()
![]() và
và ![]()
Vì ![]() nên ta chọn
nên ta chọn ![]() . Vậy
. Vậy ![]()
Câu 4:
Vì đồ thị hàm số cắt đường thẳng ![]() tại điểm có tung độ bằng 2 nên giao điểm đó có hoành độ x thỏa mãn:
tại điểm có tung độ bằng 2 nên giao điểm đó có hoành độ x thỏa mãn: ![]() hay
hay ![]()
Thay ![]() vào (1) ta có:
vào (1) ta có:
![]()
![]()
![]() .
.
Vậy để thỏa mãn điều kiện bài toán thì ![]() .
.
Câu 5:
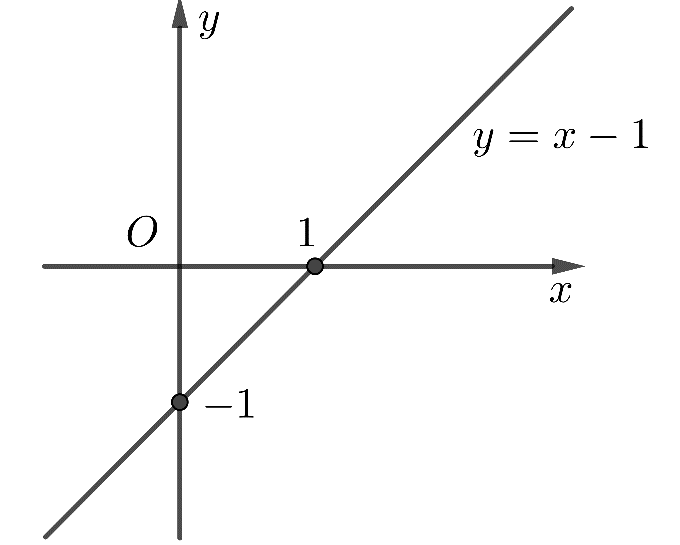
a) Bảng giá trị:
|
|
|
|
|
|
![]() Đường thẳng
Đường thẳng ![]() đi qua 2 điểm
đi qua 2 điểm ![]() và
và ![]() .
.
Đồ thị:
b) Hoành độ giao điểm của ![]() và
và ![]() là nghiệm của phương trình:
là nghiệm của phương trình:
![]() (
(![]() ).
).
![]() (*)
(*)
Để ![]() tiếp xúc
tiếp xúc ![]() thì phương trình (*) có nghiệm duy nhất khi:
thì phương trình (*) có nghiệm duy nhất khi:
![]()
![]()
![]() .
.
Vậy ![]() .
.
Câu 6:
![]() giao điểm với
giao điểm với ![]() tại 2 điểm nằm về hai phía của trục tung
tại 2 điểm nằm về hai phía của trục tung
Tọa độ giao điểm là nghiệm của phương trình:
![]()
![]()
![]() cắt
cắt ![]() tại hai điểm nằm về hai phía của trục tung khi và chỉ khi phương trình (1) có hai nghiệm trái dấu.
tại hai điểm nằm về hai phía của trục tung khi và chỉ khi phương trình (1) có hai nghiệm trái dấu.
![]()
![]()
![]() .
.
Vậy ![]() thì
thì ![]() cắt d tại hai điểm nằm về hai phía của trục tung.
cắt d tại hai điểm nằm về hai phía của trục tung.
Câu 7:
a Tìm m để đường thẳng ![]() đi qua
đi qua ![]()
Do (d) đi qua ![]() Thay
Thay ![]() vào phương trình đường thẳng ta được:
vào phương trình đường thẳng ta được:
![]()
![]()
![]()
Vậy với m = 2 thì đường thẳng ![]() đi qua
đi qua ![]()
b Tìm m để đường thẳng ![]() tiếp xúc với Parabol
tiếp xúc với Parabol ![]()
Phương trình hoành độ giao điểm của (d) và (P) là
![]()
![]()
![]()
Để ![]() tiếp xúc với Parabol
tiếp xúc với Parabol ![]() thì phương trình (*) có nghiệm kép hay
thì phương trình (*) có nghiệm kép hay
![]()
![]()
![]()
![]() hoặc
hoặc ![]()
Vậy ![]() hoặc
hoặc ![]()
Giải những bài tập khác
Giải bài tập những môn khác
Môn học lớp 9 KNTT
5 phút giải toán 9 KNTT
5 phút soạn bài văn 9 KNTT
Văn mẫu 9 kết nối tri thức
5 phút giải KHTN 9 KNTT
5 phút giải lịch sử 9 KNTT
5 phút giải địa lí 9 KNTT
5 phút giải hướng nghiệp 9 KNTT
5 phút giải lắp mạng điện 9 KNTT
5 phút giải trồng trọt 9 KNTT
5 phút giải CN thực phẩm 9 KNTT
5 phút giải tin học 9 KNTT
5 phút giải GDCD 9 KNTT
5 phút giải HĐTN 9 KNTT
Môn học lớp 9 CTST
5 phút giải toán 9 CTST
5 phút soạn bài văn 9 CTST
Văn mẫu 9 chân trời sáng tạo
5 phút giải KHTN 9 CTST
5 phút giải lịch sử 9 CTST
5 phút giải địa lí 9 CTST
5 phút giải hướng nghiệp 9 CTST
5 phút giải lắp mạng điện 9 CTST
5 phút giải cắt may 9 CTST
5 phút giải nông nghiệp 9 CTST
5 phút giải tin học 9 CTST
5 phút giải GDCD 9 CTST
5 phút giải HĐTN 9 bản 1 CTST
5 phút giải HĐTN 9 bản 2 CTST
Môn học lớp 9 cánh diều
5 phút giải toán 9 CD
5 phút soạn bài văn 9 CD
Văn mẫu 9 cánh diều
5 phút giải KHTN 9 CD
5 phút giải lịch sử 9 CD
5 phút giải địa lí 9 CD
5 phút giải hướng nghiệp 9 CD
5 phút giải lắp mạng điện 9 CD
5 phút giải trồng trọt 9 CD
5 phút giải CN thực phẩm 9 CD
5 phút giải tin học 9 CD
5 phút giải GDCD 9 CD
5 phút giải HĐTN 9 CD
Trắc nghiệm 9 Kết nối tri thức
Trắc nghiệm 9 Chân trời sáng tạo
Trắc nghiệm 9 Cánh diều
Tài liệu lớp 9
Văn mẫu lớp 9
Đề thi lên 10 Toán
Đề thi môn Hóa 9
Đề thi môn Địa lớp 9
Đề thi môn vật lí 9
Tập bản đồ địa lí 9
Ôn toán 9 lên 10
Ôn Ngữ văn 9 lên 10
Ôn Tiếng Anh 9 lên 10
Đề thi lên 10 chuyên Toán
Chuyên đề ôn tập Hóa 9
Chuyên đề ôn tập Sử lớp 9
Chuyên đề toán 9
Chuyên đề Địa Lý 9
Phát triển năng lực toán 9 tập 1
Bài tập phát triển năng lực toán 9

Bình luận