Câu 1: Trong mặt phẳng với hệ tọa độ $Oxy$, cho tam giác $ABC$ có $A( 1; 4), B(3; 2), C(7; 3)$. Viết phương trình tham số của trung tuyến $CM$ của tam giác?

• A. $\left\{\begin{matrix}x= 7 &  & \\ y= 3+ 5t &  & \end{matrix}\right.$
• B. $\left\{\begin{matrix}x= 3- 5t &  & \\ y= -7 &  & \end{matrix}\right.$

• C. $\left\{\begin{matrix}x= 7+ t &  & \\ y= 3 &  & \end{matrix}\right.$

• D. $\left\{\begin{matrix}x= 2 &  & \\ y= 3- t &  & \end{matrix}\right.$

Câu 2: Viết phương trình tổng quát của đường thẳng $d$ đi qua điểm $M( -2; -5)$ và song song với đường phân giác của góc phần tư thứ nhất?

• A. $x+ y- 3= 0$

• B. $x- y- 3= 0$

• C. $x+ y+ 3= 0$
• D. $2x- y- 1= 0$

Câu 3: Xét vị trí tương đối của hai đường thẳng 

                 $d_{1}: \left\{\begin{matrix}x= -1+ t &  & \\ y= -2-2t &  & \end{matrix}\right.$

                 $d_{2}: \left\{\begin{matrix}x= 2- 2t' &  & \\ y= -8+ 4t' &  & \end{matrix}\right.$

• A. Trùng nhau

• B. Song song
• C. Vuông góc với nhau
• D. Cắt nhau nhưng không vuông góc với nhau

Câu 4: Phương trình tổng quát của đường thẳng $\Delta$ đi qua điểm $M( ; 3)$ và có vecto pháp tuyến $\vec{n}= (5; -2)$ là:

• A. $5( x+ 1)- 2(y+ 3) = 0$

• B. $5(x-1)- 2(y- 3)= 0$

• C. $(x- 5)+ 3(y+ 2)= 0$

• D. $(x+ 5) + 3( y- 2)= 0$

Câu 5: Cho hình vuông $ABCD$ co tọa độ đỉnh $A(3; 2)$ và tâm hình vuông là $I( -1; 4)$. Khi đó phương trình của đường chéo $BD$ là?

• A. $2x- y+ 6= 0$

• B. $x+ y- 3= 0$
• C. $2x- y- 1= 0$
• D. $x- y+ 5=  0$

Câu 6: Quỹ tích các điểm cách đều hai đường thẳng 

       $d_{1}: 5x- 12y+ 4= 0$

       $d_{2}: x+ 2y+ 6= 0$ là?

• A. $9x+ 7y+ 2= 0$ và $7x- 9y= 0$
• B. $9x- 7y+ 2= 0$ và $77x- 99y+ 46= 0$
• C. $9x- 7y+ 2= 0$ và $7x+ 9y= 0$

• D. $9x+ 7y+ 2= 0$ và $77x- 99y+ 46= 0$

Câu 7: Cho ba đường thẳng 

$d_{1}: 2x- y- 1= 0$

$d_{2}: mx- (m+ 2)y+ m+ 4= 0$

$d_{3}: x+ y- 2= 0$

Giá trị của $m$ để ba đường thẳng trên đồng quy là?

• A. $m= 0$
• B. $m= 2$

• C. $m= -2$

• D. $m= 4$

Câu 8: Đường thẳng $\Delta$ tạo với đường thẳng $d: x+ 2y- 6= 0$ một góc $45^{\circ}$. Tìm hệ số góc $k$ của đường thẳng $\Delta$?

• A. $k= \frac{1}{3}$ hoặc $k= -3$

• B. $k= \frac{1}{3}$ hoặc $k= 3$
• C. $k= -\frac{1}{3}$ hoặc $k= -3$
• D. $k= -\frac{1}{3}$ hoặc $k= 3$

Câu 9: Trong mặt phẳng với hệ tọa độ $Oxy$, cho điểm $M( x_{0}, y_{0})$ và đường thẳng $\Delta: ax+ by+ c= 0$. Khoảng cách từ điểm $M$ đến $\Delta$ được tính bằng công thức nào?

• A. $d(M, \Delta): \frac{\left | ax_{0}+ by_{0} \right |}{\sqrt{a^{2}+ b^{2}}}$
• B. $d(M, \Delta): \frac{ax_{0}+ by_{0}}{\sqrt{a^{2}+ b^{2}}}$

• C. $d(M, \Delta): \frac{\left | ax_{0}+ by_{0} + c\right |}{\sqrt{a^{2}+ b^{2}}}$

• D. $d(M, \Delta): \frac{ ax_{0}+ by_{0}+ c }{\sqrt{a^{2}+ b^{2}}}$

Câu 10: Cho $\left\{\begin{matrix}M(15; 1) &  & \\ \Delta\left\{\begin{matrix}x= 2+ 3t&  & \\ y= 2+ 4t&  & \end{matrix}\right.&  & \end{matrix}\right.$ và $M'$ bất kì thuộc $\Delta$. 

Tính $MM'_{min}$?

• A. $\sqrt{ 10}$

• B. $\frac{1}{\sqrt{10}}$
• C. $\frac{16}{\sqrt{5}}$
• D. $\sqrt{5}$

Câu 11: Cho $\left\{\begin{matrix}(C): x^{2}+ y^{2}+ 8x+ 6y+ 5= 0 &  & \\ \Delta: 3x- 4y+ m= 0&  & \end{matrix}\right.$

Giá trị của $m$ để đường thẳng cắt đường tròn theo dây cung dài nhất là?

• A. $m= 0$

• B. $m= 2$
• C. $m= 4$
• D. $m= 6$

Câu 12: Đường tròn có tâm nằm trên đường thẳng $\Delta_{1}: x+ y- 3= 0$, đi qua điểm $A(-1; 3)$ và tiếp xúc với đường thẳng $\Delta_{2}: x- y+ 5= 0$ có phương trình là?

• A. $x^{2}+ y^{2}- 4x- 2y- 8= 0$

• B. $x^{2}+ y^{2}+ x- 7y+ 12= 0$

• C. $x^{2}+ y^{2}+ 2x+ 2y- 1= 0$
• D. $x^{2}+ y^{2}- 2x- 2y+ 9= 0$

Câu 13: Cho $\left\{\begin{matrix}(C): x^{2}+ y^{2}- 2x+ 2y- 14= 0 &  & \\ \Delta:-x+ 2y- 2= 0&  & \end{matrix}\right.$

Đường thẳng $\Delta$ cắt đường tròn $(C)$ theo dây cung có độ dài là?

• A. $\sqrt{11}$
• B. $2\sqrt{5}$

• C. $2\sqrt{11}$

• D. $\sqrt{3}$

Câu 14: Có bao nhiêu đường thẳng đi qua điểm $M( -2; 0)$ tiếp xúc  với đường tròn $(C): (x- 2)^{2}+ (y+ 3)^{2}= 4$?

• A. 0
• B. 1

• C. 2

• D. vô số

Câu 15: Phương trình chính tắc của elip có độ dài trục nhỏ bằng 12, độ dài tiêu cự bằng 8 là?

• A. $\frac{x^{2}}{36}+ \frac{y^{2}}{20}= 1$

• B. $\frac{x^{2}}{52}+ \frac{y^{2}}{36}= 1$

• C. $\frac{x^{2}}{208}+ \frac{y^{2}}{144}= 1$
• D.$\frac{x^{2}}{144}+ \frac{y^{2}}{80}= 1$

Câu 16: Cho elip có phương trình: $\frac{x^{2}}{16}+ \frac{y^{2}}{7}= 1$. Đường thẳng $x= 1$ cắt elip theo dây cung có độ dài là: 

• A. $\frac{\sqrt{105}}{2}$

• B. $\frac{\sqrt{87}}{2}$
• C. $\frac{\sqrt{53}}{2}$
• D. $\frac{\sqrt{19}}{2}$

Câu 17: Cho elip có phương trình $\frac{x^{2}}{16}+ \frac{y^{2}}{9}= 1$. Diện tích của một hình tròn nằm gọn bên trong elip nhận giá trị nào sau đây?

• A. $9\pi$

• B. 27

• C. 30
• D. $10\pi$

Câu 18: Cho elip $(E)$: $\frac{x^{2}}{25}+ \frac{y^{2}}{9}= 1$. Hai điểm  $A, B$ là hai đỉnh của elip lần lượt nằm trên hai trục $Ox, Oy$. Khi đó độ dài đoạn thẳng $AB$ bằng?

• A. 34

• B. $\sqrt{34}$

• C. 5
• D. $\sqrt{136}$

Câu 19: Cho điểm $M(2; 3)$ nằm trên elip $(E)$: $\frac{x^{2}}{a^{2}}+ \frac{y^{2}}{b^{2}}= 1$. Trong các điểm sau điểm nào không nằm trên $(E)$? 

• A. $M_{1}( -2; 3)$
• B. $M_{2}(2; -3)$
• C. $M_{3}(-2; -3)$

• D. $M_{4}(3; 2)$

Câu 20: Một elip $(E)$ có khoảng cách giữa hai đỉnh kế tiếp nhau gấp $\frac{3}{2}$ lần tiêu cự của nó. Tỉ số $e$ của tiêu cự với độ dài trục lớn bằng:

• A. $e= \frac{\sqrt{5}}{5}$

• B. $e= \frac{2}{5}$
• C. $e= \frac{\sqrt{3}}{5}$
• D. $e= \frac{\sqrt{2}}{5}$

Câu 21: Cho đường tròn $(C)$ tâm $O$ bán kính $OB$ nội tiếp elip $(E)$ có một tiêu điểm $F( -4; 0)$, độ dài trục lớn là 10. Viết phương trình đường tròn $(C)$?

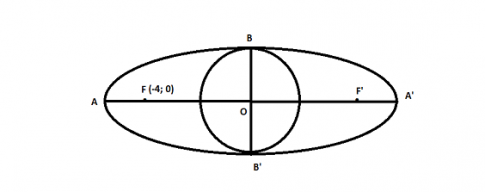
• A. $x^{2}+ y^{2}= 16$

• B. $x^{2}+ y^{2}= 9$

• C. $x^{2}+ y^{2}= 6$
• D. $x^{2}+ y^{2}- 6y= 0$

Câu 22: Tìm phương trình chính tắc của elip nếu phương trình đường chuẩn của nó là $ 5x= \pm 3$ và độ dài trục lớn là 10?

• A. $\frac{x^{2}}{81}+ \frac{y^{2}}{64}= 1$
• B. $\frac{x^{2}}{25} - \frac{y^{2}}{9}= 1$
• C. $\frac{x^{2}}{25}+ \frac{y^{2}}{16}= 1$

• D. $\frac{x^{2}}{25}+ \frac{y^{2}}{9}= 1$

Câu 23: Tìm phương trình chính tắc của elip đi qua điểm (6; 0) và có tâm sai bằng $\frac{1}{2}$

• A. $\frac{x^{2}}{36}+ \frac{y^{2}}{27}= 1$

• B. $\frac{x^{2}}{6}+ \frac{y^{2}}{3}= 1$
• C. $\frac{x^{2}}{3}+ \frac{y^{2}}{2}= 1$
• D. $\frac{x^{2}}{36}+ \frac{y^{2}}{18}= 1$

Câu 24: Đường thẳng qua $M( 1; 1)$ và cắt elip $(E): 4x^{2}+ 9y^{2}= 36$ tại hai điểm $M_{1}, M_{2}$ sao cho $MM_{1}= MM_{2}$ có phương trình là?

• A. $2x+ 4y- 5= 0$

• B. $4x+ 9y- 13= 0$

• C. $x+ y+ 5= 0$
• D. $16x- 15y+ 100= 0$

Câu 25: Biết $(E)$ có các tiêu điểm $F_{1}( -\sqrt{7}; 0), F_{2}(\sqrt{7}; 0)$ và đi qua điểm $M( -\sqrt{7}; \frac{9}{4})$. Gọi $N$ là điểm đối xứng với $M$ qua gốc tọa độ. Khi đó: 

• A. $NF_{1}+ MF_{2}= \frac{9}{2}$
• B. $NF_{2}+ MF_{1}= \frac{23}{2}$
• C. $NF_{2}.NF_{1}= \frac{7}{2}$

• D. $NF_{1}+ MF_{1}= 8$