BÀI TẬP CUỐI CHƯƠNG VI (1 tiết)

I. ÔN TẬP KIẾN THỨC ĐÃ HỌC TRONG CHƯƠNG II

+ Nhóm 1:

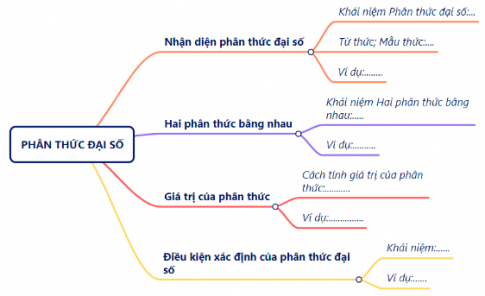
+ Nhóm 2:

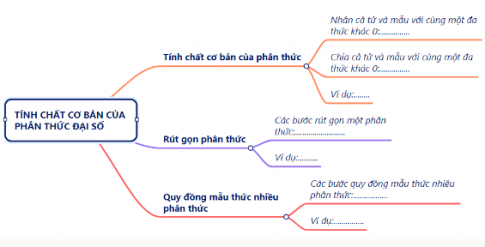
+ Nhóm 3:

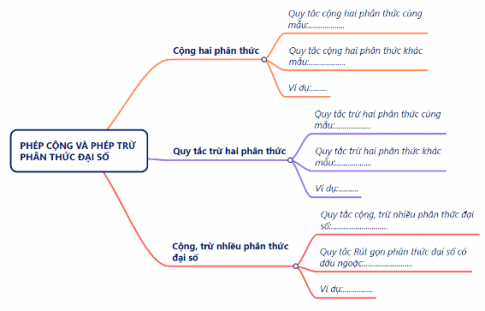
+ Nhóm 4:

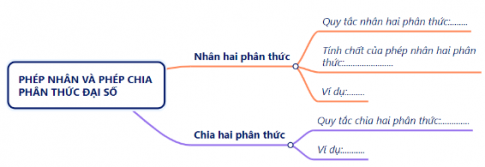
II. BÀI TẬP LUYỆN TẬP

6.41

a) 

P=$\frac{x}{x^{2}-2x+4}$-$\frac{1}{x+2}$=$\frac{x(x+2)-(x^{2}-2x+4)}{(x+2)(x^{2}-2x+4)}$=$\frac{4(x-1)}{x^{3}+8}$

b) 

P=$\frac{16}{x-2}$-$\frac{4(x-2)}{x+2}$=$\frac{16(x+2)+4(x-2)^{2}}{(x-2)(x+2)}$=$\frac{4(x^{2}+12)}{x^{2}-4}$

c) 

P=$\frac{x^{2}-4x+4}{x^{2}-9}$:$\frac{x-2}{x+3}$=$\frac{(x-2)^{2}}{(x-3)(x+3)}$.$\frac{x+3}{x-2}$=$\frac{x-2}{x-3}$

d) 

P=$\frac{x^{2}-4}{x^{2}+3x}$.$\frac{x^{2}-9}{2x+4}$=$\frac{(x-2)(x+2)}{x(x+3)}$.$\frac{(x+3)(x-3)}{2(x+2)}$=$\frac{(x-2)(x-3)}{2x}$

6.42

a) 

$\frac{2}{3x}$+$\frac{x}{x-1}$+$\frac{6x^{2}-4}{2x(1-x)}$=$\frac{2}{3x}$+$\frac{-x}{1-x}$+$\frac{3x^{2}-2}{x(1-x)}$

=$\frac{2(1-x)+(-x)3x+3(3x^{2}-2)}{3x(1-x)}$=$\frac{6x^{2}-2x-4}{3x(1-x)}$

b) 

$\frac{x^{3}+1}{1-x^{3}}$+$\frac{x}{x-1}$-$\frac{x+1}{x^{2}+x+1}$=$\frac{-x^{3}-1}{x^{3}-1}$+$\frac{x(x^{2}+x+1)-(x+1)(x-1)}{(x-1)(x^{2}+x+1)}$

=$\frac{-x^{3}-1+(x^{3}+x^{2}+x)-(x^{2}-1)}{(x-1)(1+x+x^{2})}$=$\frac{x}{x^{3}-1}$

c) 

($\frac{2}{x+2}$-$\frac{2}{1-x}$).$\frac{x^{2}-4}{4x^{2}-1}$=$\frac{2[(1-x)-(x+2)]}{(x+2)(1-x)}$.$\frac{(x+2)(x-2)}{(2x-1)(2x+1)}$

=$\frac{2(-2x+1)(x-2)}{(x-1)(2x-1)(2x+1)}$=-$\frac{2(x-2)}{(1-x)(2x-1)}$=$\frac{2(x-1)}{(x-1)(2x-1)}$

d)

1+$\frac{x^{3}-x}{x^{2}+1}$.($\frac{1}{1-x}$-$\frac{1}{1-x^{2}}$)=1+$\frac{x(x^{2}-1)}{x^{2}+1}$.$\frac{1+x-1}{(1-x)(1+x)}$

=1+$\frac{-x^{2}(1-x^{2})}{(x^{2}+1)(1-x^{2})}$=1-$\frac{x^{2}}{x^{2}+1}$=$\frac{1}{x^{2}+1}$

- Đáp án câu hỏi trắc nghiệm