BÀI 39. HÌNH CHÓP TỨ GIÁC ĐỀU (2 tiết)

I. HÌNH CHÓP TỨ GIÁC ĐỀU

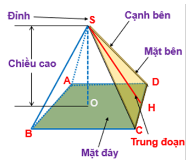
Hình chóp tứ giác S.ABCD

HĐ1:

Đỉnh là: S. Các cạnh bên là SA, SB, SC, SD 

HĐ2:

Đường cao là SO. Trung đoạn là SH   

HĐ3:

Các mặt bên các tam giác SAB, SBC, SCD, SDA và mặt đáy là ABCD

Nhận xét

Hình chóp tứ giác đều có:

+ Đáy là hình vuông, các mặt bên là các tam giác cân bằng nhau có chung đỉnh;

+ Chân đường cao kẻ từ đỉnh tới mặt đáy là điểm cách đều các đỉnh của mặt đáy (giao điểm hai đường chéo).

Ví dụ 1: SGK – tr.117

Hướng dẫn giải: SGK – tr.117

Thực hành

Hướng dẫn thực hiện: SGK – tr.118

II. DIỆN TÍCH XUNG QUANH VÀ THỂ TÍCH CỦA HÌNH CHÓP TỨ GIÁC ĐỀU

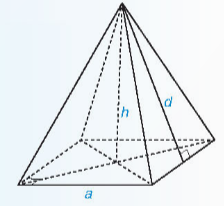
- Diện tích xung quanh bằng tích của nửa chu vi đáy với trung đoạn.

S$_{xq}$=p . d

Trong đó p là nửa chu vi đáy, d là trung đoạn.

- Thể tích bằng $\frac{1}{3}$ tích của diện tích đáy với chiều cao của nó.

V=$\frac{1}{3}$S.h

Ví dụ 2: SGK – tr.119

Hướng dẫn giải: SGK – tr.119

Luyện tập 1

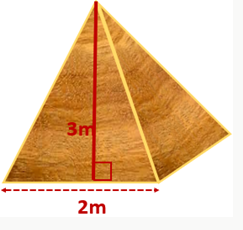
Diện tích xung quanh bốn mặt khối gỗ là: S$_{xq}$=p.d=(2.4).$\frac{1}{2}$.3=12 (cm$^{2}$)

Số tiền bác Khôi phải trả để sơn 4 mặt xung quanh là: 12 . 30 000=360 000 (đồng)

Luyện tập 2

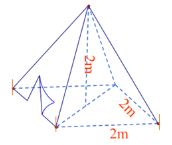
a) Thể tích là V=$\frac{8}{3}$ m$^{3}$

b) Diện tích xung quanh của lều là:

 S$_{xq}$=8,96 m$^{2}$

Diện tích đáy lều là S$_{đáy}$=2$^{2}$=4 m$^{2}$

Diện tích vải bạt cần dùng là: 

S=8,96+4=12,96 m$^{2}$ 

Vận dụng

Kim tự tháp Kheops có thể tích là:

V = $\frac{1}{3}$.230.230.147=2 592 100 (cm$^{3}$)