BÀI 35. ĐỊNH LÍ PYTHAGORE VÀ ỨNG DỤNG (2 tiết)

I. ĐỊNH LÍ PYTHAGORE

HĐ1

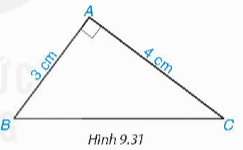
BC=5 

Ta thấy 3$^{2}$+4$^{2}$=5$^{2}$ hay AB$^{2}$+AC$^{2}$=BC$^{2}$ 

HĐ2

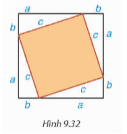
- Phần không bị che khuất là hình vuông.

- Tổng diện tích bốn ta, giác vuông:

4.$\frac{1}{2}$.ab=2ab 

- Diện tích tấm bìa: (a+b).(a+b)=(a+b)$^{2}$

- Ta có: (a+b)$^{2}$=c$^{2}$+2ab

Vậy a$^{2}$+b$^{2}$=c$^{2}$.

Định lí Pythagore

Trong một tam giác vuông, bình phương cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.

Chứng minh định lí (SGK – tr.94)

Chú ý:

Nếu tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông.

Lưu ý: Bình phương của một đoạn thẳng là bình phương độ dài của đoạn thẳng đó.

Câu hỏi

+) x$^{2}$=1$^{2}$+1$^{2}$=2 

=> x=$\sqrt{2}$

+) ($\sqrt{5}$)$^{2}$=1+y$^{2}$

=> y$^{2}$=4 => y=2

Ví dụ 1: (SGK – tr.94)

Hướng dẫn giải (SGK – tr.94)

Luyện tập 1

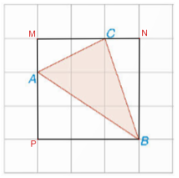
+ Qua C kẻ MN; qua B kẻ BP sao cho MN//BP và MN=BP.

+ Qua A kẻ MP; qua B kẻ BN sao cho MP//BN và MP=BN

Ta có MNBP là hình vuông. 

+ Áp dụng định lí Pythagore vào các tam giác vuông AMC;CNB;APB ta có:

AC$^{2}$=1$^{2}$+2$^{2}$=5 => AC=$\sqrt{5}$ cm

AB$^{2}$=2$^{2}$+3$^{2}$=13 => AB=$\sqrt{13}$ cm

BC$^{2}$=1$^{2}$+3$^{2}$=10 => BC=$\sqrt{10}$ cm

Vận dụng 1

- Nếu điểm M biểu diễn cho số thực x

=> OM có độ dài là x (đvđd).

- OM là cạnh huyền của một tam giác vuông; 2 cạnh góc vuông là hai cạnh của hình chữ nhật.

=> Áp dụng định lí Pythagore, có:

x$^{2}$=1$^{2}$+3$^{2}$=10 => x=$\sqrt{10}$.

II. ỨNG DỤNG CỦA ĐỊNH LÍ PYTHAGORE

Tính độ dài đoạn thẳng

Bài toán 1 (SGK – tr.95)

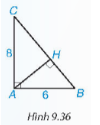
Hướng dẫn giải (SGK – tr.95)

Nhận xét

Nếu tam giác ABC vuông tại A có đường cao AH=h, các cạnh BC=a;AC=b;AB=c thì: h . a=b . c

Luyện tập 2

- Ta có: x$^{2}$+12$^{2}$=13$^{2}$ 

=> x$^{2}$=13$^{2}$-12$^{2}$=25

=> x=5.

Vậy ∆ABC=∆EDF (cạnh huyền – cạnh góc vuông)

∆ABC $\sim $ ∆MPN (c.c.c)

=> $\frac{MP}{ED}$=$\frac{MP}{AB}$=$\frac{PN}{BC}$=$\frac{PN}{DF}$. Do đó: ∆MPN $\sim $ ∆EDF (cạnh huyền – cạnh góc vuông)

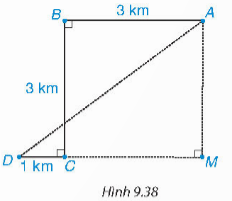
Vận dụng 2

- Do ABCM là hình vuông nên AM=BC=3 km; MC=AB=3 km.

=> MD=MC+CD=4 km

- Áp dụng định lí Pythagore cho ∆AMD, ta có:

AD$^{2}$=AM$^{2}$+MD$^{2}$=25

=> AD=5 km.

Chứng minh tính chất hình học

Bài toán 2: (SGK – tr.96)

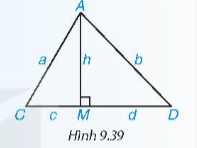
Hướng dẫn giải (SGK – tr.96)

Chú ý

- Trong bài toán 2, nếu gọi AM là đường cao, các đoạn thẳng AC, AD là đường xiên thì đoạn thẳng MC được gọi là hình chiếu của đường xiên AC và đoạn thẳng MD được gọi là hình chiếu của đường xiên AD.

- Với cùng 1 đường cao, hình chiếu cảng lớn thì đường xiên càng lớn.

Câu hỏi

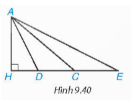
- Do HD<HC<HE nên AD<AC<AE. Vậy đoạn AE có độ dài lớn nhất.

Luyện tập 3

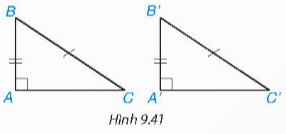
∆ABC vuông tại A, có: BC$^{2}$=AB$^{2}$+AC$^{2}$ (1)

∆A'B'C' vuông tại A', có: B'C'$^{2}$=A'B'$^{2}$+A'C'$^{2}$ (2)

Mà AB=A'B';BC=B'C' (3)

Từ (1)(2)(3) suy ra: AC=A'C'

Vậy ∆ABC=∆A'B'C' (c.c.c)

Thử thách nhỏ

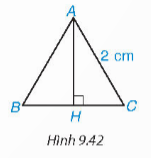
Áp dụng định lí Pythagore cho ∆ABH có:

AB$^{2}$=AH$^{2}$+BH$^{2}$

=> AH$^{2}$=AB$^{2}$-BH$^{2}$

AH$^{2}$=3 => AH=$\sqrt{3}$≈1,73 (cm)