Lý thuyết trọng tâm toán 8 cánh diều bài 6: Trường hợp đồng dạng thứ nhất của tam giác
Tổng hợp kiến thức trọng tâm toán 8 cánh diều bài 6: Trường hợp đồng dạng thứ nhất của tam giác. Tài liệu nhằm củng cố, ôn tập lại nội dung kiến thức bài học cho học sinh dễ nhớ, dễ ôn luyện. Kéo xuống để tham khảo
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
I. TRƯỜNG HỢP ĐỒNG DẠNG THỨ NHẤT CỦA TAM GIÁC
HĐ1
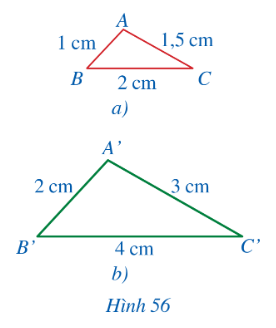
$\frac{A'B'}{AB}=\frac{A'C'}{AC}=\frac{B'C'}{BC}$ vì $\frac{2}{1}=\frac{3}{1,5}=\frac{4}{2}$ = 2
Định lí: Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng với nhau.
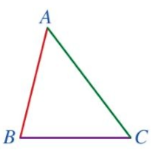
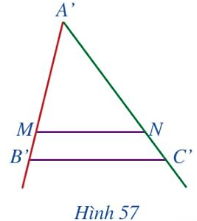
GT | ∆ABC, ∆A'B'C', $\frac{A'B'}{AB}=\frac{A'C'}{AC}=\frac{B'C'}{BC}$ |
KL | ∆A'B'C'∽∆ABC |
Chứng minh: SGK – tr.74
Ví dụ 1: SGK – tr.75
Hướng dẫn giải: SGK – tr .75
Luyện tập 1
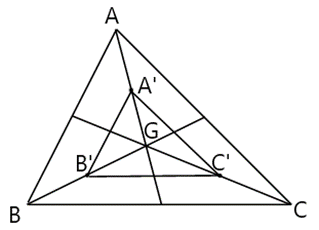
Do A', B', C' lần lượt là trung điểm các cạnh AG, BG, CG nên A'B'; B'C'; C'A' lần lượt là đường trung bình của các ∆AGB; ∆BGC; ∆CGA
Theo tính chất đường trung bình của tam giác, suy ra: $\frac{A'B'}{AB}=\frac{A'C'}{AC}=\frac{B'C'}{BC}=\frac{1}{2}$.
Vì vậy ΔA'B'C' ∽ ΔABC (c.c.c).
Ví dụ 2: SGK – tr.75
Hướng dẫn giải: SGK – tr.76
II. ÁP DỤNG TRƯỜNG HỢP ĐỒNG DẠNG THỨ NHẤT CỦA TAM GIÁC VÀO TAM GIÁC VUÔNG
HĐ2
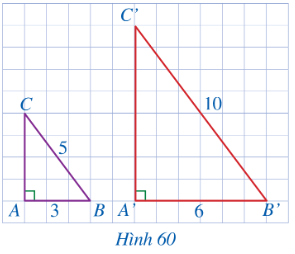
a) CA = 4; C’A’ = 8
b) $\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{C'A'}{CA}$
c) ΔA'B'C' ∽ ΔABC
Định lí: Nếu cạnh huyền và một cạnh góc vuông của tam giác này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
GT | ∆ABC, ∆A'B'C', $\widehat{A'}=\widehat{A}=90^{o}$ $\frac{B'C'}{BC}=\frac{A'B'}{AB}$ |
KL | ∆A'B'C' ∽ ∆ABC |
Chứng minh định lí: SGK – tr.76+77
Ví dụ 3: SGK – tr.77
Hướng dẫn giải: SGK – tr.77
Ví dụ 4: SGK – tr.77
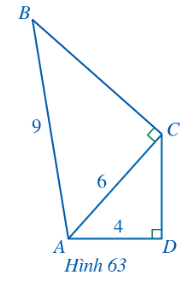
Hướng dẫn giải: SGK – tr.77+78
Luyện tập 2
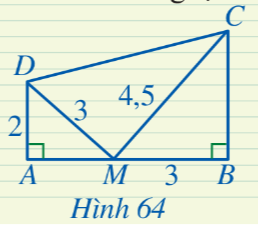
Xét ΔBCM và ΔAMD, ta có:
$\frac{MB}{AD}=\frac{MC}{DM}$ vì $\frac{3}{2}=\frac{4,5}{3}$
Suy ra: ΔBCM ∽ ΔAMD (cạnh huyền – cạnh góc vuông)
Suy ra $\widehat{BMC}=\widehat{ADM}$ (1)
Mà $\widehat{ADM}+\widehat{AMD}=90^{\circ}$ (2)
Từ (1) và (2) suy ra $\widehat{AMD}+\widehat{BMC}=90^{\circ}$ (3)
Mà $\widehat{AMD}+\widehat{DMC}+\widehat{BMC}=180^{\circ}$ (4)
Từ (3) và (4) suy ra $\widehat{DMC}$ = 90°
Suy ra ΔCDM vuông tại M. (đpcm)
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây

Bình luận