Lý thuyết trọng tâm toán 8 cánh diều bài 2: Ứng dụng của định lí Thalès trong tam giác
Tổng hợp kiến thức trọng tâm toán 8 cánh diều bài 2: Ứng dụng của định lí Thalès trong tam giác. Tài liệu nhằm củng cố, ôn tập lại nội dung kiến thức bài học cho học sinh dễ nhớ, dễ ôn luyện. Kéo xuống để tham khảo
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
I. ƯỚC LƯỢNG KHOẢNG CÁCH
Ví dụ 1: (SGK – tr.58)
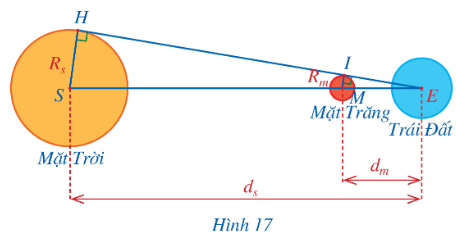
Xét ∆EHS có $\widehat{EIM}=\widehat{EHS}=90^{o}$
=> MI // SH
Do đó, áp dụng hệ quả của định lí Thalès, có: $\frac{MI}{SH}=\frac{EM}{ES}$.
Vậy $\frac{R_{m}}{R_{s}}=\frac{d_{m}}{d_{s}}$.
Các nhà toán học và thiên văn học Hy Lạp cổ đại đã sử dụng hệ thức trên và một số hệ thức có được từ hiện tượng Nguyệt thực để ước lượng bán kính của Mặt Trời, Trái Đất, Mặt Trăng cũng như khoảng cách từ Trái Đất đến Mặt Trăng và Mặt Trời.
Ví dụ 2: (SGK – tr.59)
|
|
Hướng dẫn giải (SGK – tr.59)
Luyện tập 1
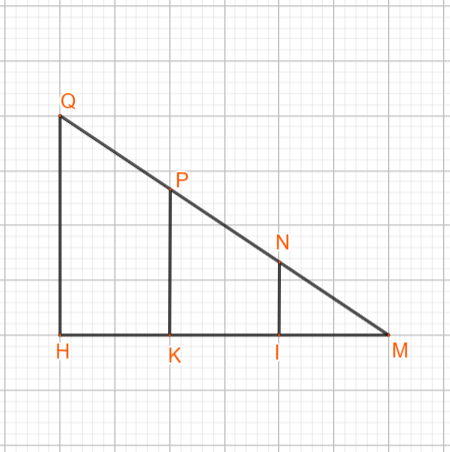
Giả sử bàn cờ vua được mô tả bởi bảng ô vuông 8×8 như hình vẽ dưới. Cái que là đoạn MQ
Xét các điểm N, P vừa thuộc đoạn MQ vừa thuộc các đường lưới ô vuông.
Gọi I, H, K là hình chiếu của N, P, Q lên MH (xem hình dưới).
Từ đó theo hệ quả định lí Thalès có: MN = NP = PQ
II. ƯỚC LƯỢNG CHIỀU CAO
Ví dụ 3: (SGK – tr.60)
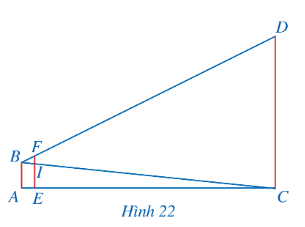
Hướng dẫn giải (SGK – tr.60)
Luyện tập 2
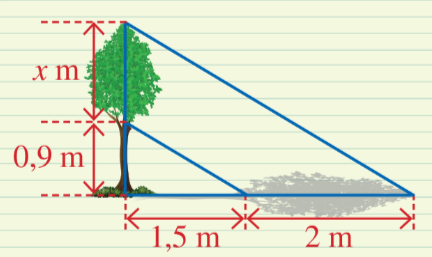
Vì các tia nắng song song với nhau (giả thiết) nên ta có tỉ lệ: $\frac{0,9}{x}=\frac{1,5}{2}$
=> x = $\frac{0,9.2}{1,5}$ = 1,2 (m)
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
Nội dung quan tâm khác
Thêm kiến thức môn học
Giải bài tập những môn khác
Giải sgk lớp 8 cánh diều
Giải SBT lớp 8 kết nối tri thức
Giải SBT lớp 8 chân trời sáng tạo
Soạn SBT lớp 8 cánh diều
Trắc nghiệm 8 Kết nối tri thức
Trắc nghiệm 8 Chân trời sáng tạo
Trắc nghiệm 8 Cánh diều
Bộ đề thi, đề kiểm tra lớp 8 chân trời sáng tạo
Giáo án lớp 8
Bình luận