I. MẶT PHẲNG TỌA ĐỘ.

HĐ1

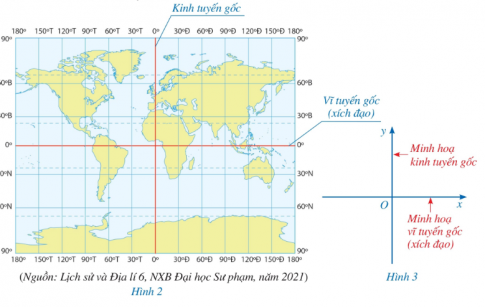
Hai đường thẳng màu đỏ trong Hình 2 được biểu diễn bởi hai trục Ox, Oy trên mặt phẳng ở Hình 3.

Khi đó, hai trục Ox, Oy trong Hình 3 vuông góc với nhau.

Định nghĩa

• Trên mặt phẳng, ta vẽ hai trục số Ox, Oy vuông góc với nhau và cắt nhau tại gốc O của mỗi trục. Khi đó ta có hệ trục tọa độ Oxy. 
• Trục Ox, Oy gọi là trục tọa độ. Ox gọi là trục hoành, Oy gọi là trục tung. O gọi là gốc tọa độ.
• Mặt phẳng có hệ trục tọa độ Oxy gọi là mặt phẳng tọa độ Oxy.

Lưu ý: Hai trục tọa độ chia mặt phẳng thành bốn góc: góc phần tư thứ I, góc phần tư thứ II, góc phần tư thứ III, góc phần tư thứ IV theo thứ tự ngược chiều kim đồng hồ.

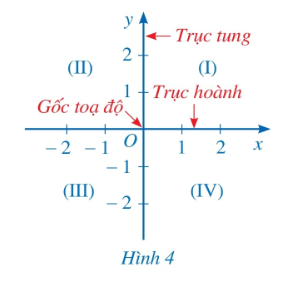
Chú ý: Các đơn vị độ dài trên hai trục tọa độ được chọn bằng nhau (nếu không có lưu ý gì thêm).

Ví dụ 1: (SGK – tr.61)

Hướng dẫn giải (SGK – tr.61)

II. TỌA ĐỘ CỦA MỘT ĐIỂM TRONG MẶT PHẲNG TỌA ĐỘ.

HĐ2

a) Hình chiếu của điểm M trên trục hoành Ox là điểm 4 trên trục Ox.

b) Hình chiếu của điểm M trên trục hoành Oy là điểm 3 trên trục Oy.

Chú ý: Cặp Cặp số (4;3) gọi là tọa độ điểm M trong mặt phẳng tọa độ.

Định nghĩa

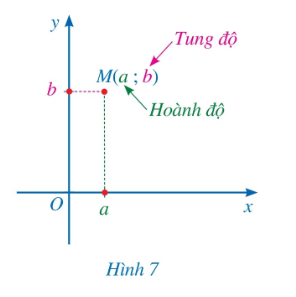
Cho điểm M trong mặt phẳng tọa độ Oxy

Giả sử hình chiếu của điểm M lên trục hoành Ox là điểm a trên trục số Ox, hình chiếu của điểm M lên trục tung Oy là điểm b trên trục Oy.

Cặp số (a; b) gọi là tọa độ của điểm M, a là hoành độ và b là tung độ của điểm M.

Điểm M có tọa độ (a; b) được kí hiệu M(a; b).

Chú ý: Trong mặt phẳng tọa độ Oxy, mỗi điểm M xác định một cặp số (a;b). Ngược lại, mỗi cặp số (a;b) xác định một điểm M.

Ví dụ 2: (SGK – tr.62).

Hướng dẫn giải (SGK – tr.62)

Nhận xét

• Điểm nằm trên trục hoành có tung độ bằng 0.
• Điểm nằm treent rục tung có hoành độ bằng 0.

Ví dụ 3: (SGK – tr.62).

Hướng dẫn giải (SGK – tr.62).

Luyện tập 1

Cách xác định các điểm trong mặt phẳng tọa độ Oxy là:

Xác định điểm A(-1; 2):

• Qua điểm – 1 trên trục Ox, ta kẻ đường thẳng vuông góc với trục Ox.
• Qua điểm 2 trên trục Oy, ta kẻ đường thẳng vuông góc với trục Oy.
• Hai đường thẳng trên cắt nhau tại điểm A(- 1; 2).

Xác định điểm B(2; 2):

• Qua điểm 2 trên trục Ox, ta kẻ đường thẳng vuông góc với trục Ox.
• Qua điểm 2 trên trục Oy, ta kẻ đường thẳng vuông góc với trục Oy.
• Hai đường thẳng trên cắt nhau tại điểm B(2; 2).

Xác định điểm C(2; 0):

• Qua điểm 2 trên trục Ox, ta kẻ đường thẳng vuông góc với trục Ox.
• Đường thẳng thẳng này cắt trục Ox tại điểm C(2; 0).

Cách xác định điểm D(0; -2):

• Qua điểm -2 trên trục Oy, ta kẻ đường thẳng vuông góc với trục Oy.
• Đường thẳng thẳng này cắt trục Oy tại điểm D(0; - 2).

Xác định điểm E($\frac{1}{2};\frac{-3}{4}$):

• Qua điểm $\frac{1}{2}$ trên trục Ox, ta kẻ đường thẳng vuông góc với trục Ox.
• Qua điểm $\frac{-3}{4}$ trên trục Oy, ta kẻ đường thẳng vuông góc với trục Oy
• Hai đường thẳng trên cắt nhau tại điểm E($\frac{1}{2};\frac{-3}{4}$)

III. ĐỒ THỊ CỦA HÀM SỐ

HĐ3

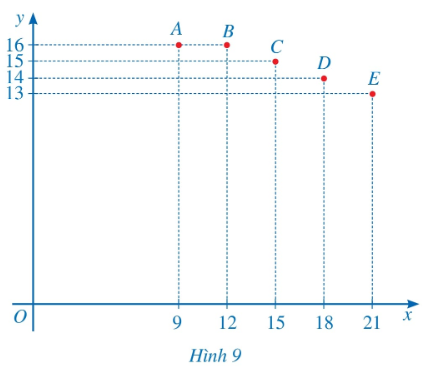
Trong mặt phẳng tọa độ Oxy, biểu diễn các điểm có tọa độ là các cặp số (x; y) tương ứng ở Bảng 1 là:

A(9; 16); B(12; 16); C(15; 15);  

D(18; 14); E(21; 13). 

Ta biểu diễn các điểm trên mặt phẳng tọa độ như sau:

HĐ4

a) Hàm số y = 2x

• Với $x_{1} = -1$ => $y_{1} = 2.(-1)= -2$
• Với $x_{2} = 1$ => $y_{2} = 2.1= 2$
• Với $x_{3} = \frac{3}{2}$ => $y_{3} = 2.\frac{3}{2}$= 3

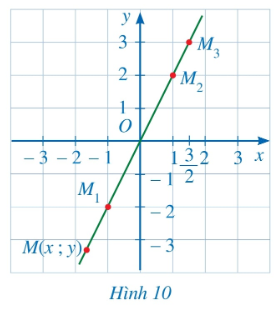
b) Như vậy tọa độ của các điểm lần lượt sẽ là: $M_{1}\left ( -1; -2\right ), M_{2}\left ( 1; 2\right ), M_{3}\left (\frac{3}{2} ;3\right )$.

Ta biểu diễn trong mặt phẳng tọa độ Oxy như sau: 

Nhận xét: 

• Với mỗi giá trị của biến số x, ta có thể xác định được một điểm M(x;y) với y = 2x trong mặt phẳng tọa độ Oxy.
• Khi biến số x thay đổi, điểm M(x; y) sẽ thay đổi theo trong mặt phẳng tọa độ Oxy và tạo nên đồ thị của hàm số y = 2x.

Khái niệm: Đồ thị của hàm số y = f(x) là tập hợp tất cả các điểm biểu diễn các cặp giá trị tương ứng (x; f(x)) trên mặt phẳng tọa độ.

Ví dụ 4: (SGK – tr.63)

Hướng dẫn giải (SGK – tr.63)

Luyện tập 2

Quan sát bảng 2 ta thấy:

• Với x = 2 thì y = 3 => Điểm A(2; 3) thuộc đồ thị hàm số.
• Với x = 5 thì y = 7 => điểm B(5; 6) không thuộc đồ thị hàm số.