I. ĐOẠN THẲNG TỶ LỆ

HĐ1

Ta có: $\frac{AB}{CD}=\frac{2}{3}$; $\frac{MN}{PQ}=\frac{4}{6}=\frac{2}{3}$

Suy ra: $\frac{AB}{CD}=\frac{MN}{PQ}$.

Kết luận: Hai đoạn thẳng AB và CD tỉ lệ với hai đoạn thẳng MN và PQ nếu có tỉ lệ thức $\frac{AB}{CD}=\frac{MN}{PQ}$.

Ví dụ 1: (SGK – tr.52)

Hướng dẫn giải (SGK – tr.52)

II. ĐỊNH LÍ THALÈS TRONG TAM GIÁC

1. Định lí Thalès

HĐ2

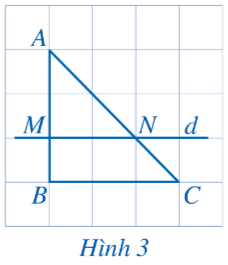
a) Quan sát Hình 3 ta thấy d // BC

b) Ta có: $\frac{AM}{MB}=\frac{AN}{NC}=2$

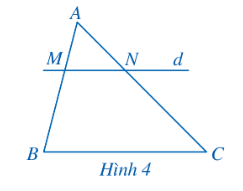
Cho ∆ABC, có d // BC, d ∩ AB = {M}, d ∩ AC = {N}

Đường thẳng d định ra trên cạnh AB hai đoạn AM, MB và định ra trên cạnh AC hai đoạn thẳng tương ứng là AN, NC.

Định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.

Nhận xét:

Trong Hình 4, nếu MN // BC thì $\frac{AM}{MB}=\frac{AN}{NC}$

Do đó $\frac{AM}{AN}=\frac{MB}{NC}=\frac{AM+MB}{AN+NC}=\frac{AB}{AC}$

Suy ra $\frac{AM}{AB}=\frac{AN}{AC}$.

Luyện tập 1

Nếu MN // AB thì $\frac{AM}{MB}=\frac{AN}{NC}$.

Do đó: $\frac{AM}{AN}=\frac{MB}{NC}=\frac{AM+MB}{AN+NC}=\frac{AB}{AC}$

Suy ra: $\frac{MB}{AB}=\frac{NC}{AC}$.

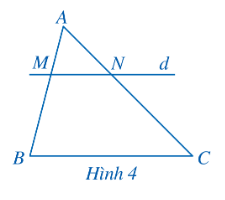
Ví dụ 2: (SGK – tr.53)

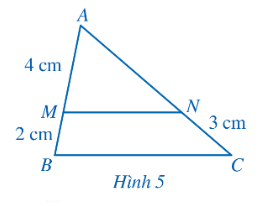
Hướng dẫn giải (SGK – tr.53)

Luyện tập 2

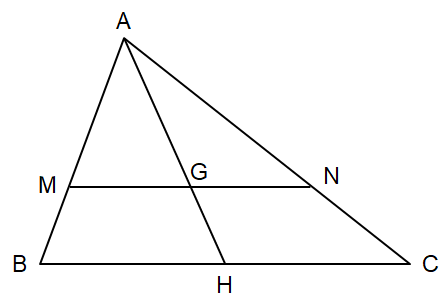
Gọi H là trung điểm của BC.

Vì G là trọng tâm tam giác ABC nên $\frac{AG}{AH}=\frac{2}{3}$ (1)

Tam giác ABH có GM // BC nên $\frac{AM}{AB}=\frac{AG}{AH}$ (định lí Thalès) (2)

Tam giác ACH có GN // BC nên $\frac{AN}{AC}=\frac{AG}{AH}$ (định lí Thalès) (3)

Từ (1), (2), (3) suy ra: $\frac{AM}{AB}=\frac{AN}{AC}=\frac{2}{3}$.

Ví dụ 3: (SGK – tr.54)

Hướng dẫn giải (SGK – tr.54)

2. Định lí Thalès đảo

HĐ3

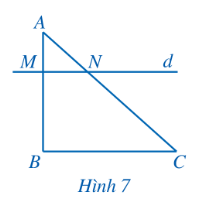
a) $\frac{AM}{MB}=\frac{AN}{NC}$.

b) Đường thẳng d (đi qua M, N) song song với BC.

Định lí Thalès đảo: Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó sóng ong với cạnh còn lại của tam giác.

Nhận xét: Trong Hình 8, nếu có một trong hai tỉ lệ thức: $\frac{AM}{AB}=\frac{AN}{AC}$; $\frac{MB}{AB}=\frac{NC}{AC}$ thì ta có MN // BC.

Ví dụ 4: (SGK – tr.55)

Hướng dẫn giải (SGK – tr.55)

Luyện tập 3

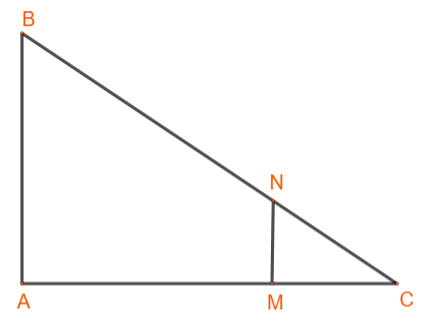
Ta có: $\frac{CM}{CA}=\frac{1}{4}$; $\frac{CN}{CB}=\frac{1,25}{5}=\frac{1}{4}$

=> MN // AB => MN ⊥ AC hay ∆NMC vuông tại M.

Áp dụng định lí Pythagore cho ∆NMC có:

MN$^{2}$ + MC$^{2}$ = NC$^{2}$

MN$^{2}$ + 1$^{2}$ = 1,25$^{2}$ 

MN = 0,75 

3. Hệ quả của định lí Thalès

Hệ quả: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.

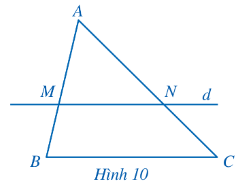
Cho ∆ABC, đường thẳng d song song với cạnh BC lần lượt cắt cạnh AB, AC tại M và N (Hình 10). Khi đó, ta có: $\frac{AM}{AB}=\frac{AN}{AC}=\frac{MN}{BC}$.

Chứng minh hệ quả: (SGK – tr.55)

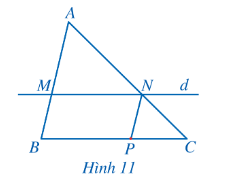
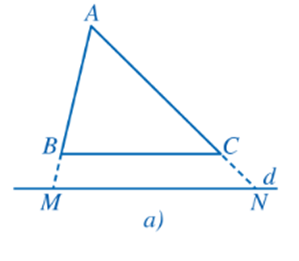
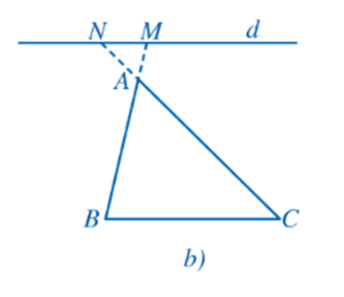
Chú ý: Hệ quả trên vẫn đúng cho trường hợp đường thẳng d song song với một cạnh của tam giác và cắt phần kéo dài của hai cạnh còn lại.

=> Ta cũng có tỉ số: $\frac{AM}{AB}=\frac{AN}{AC}=\frac{MN}{BC}$ cho hai trường hợp trên.

Ví dụ 5: (SGK – tr.56)

Hướng dẫn giải (SGK – tr.56)

Ví dụ 6: (SGK – tr.56)

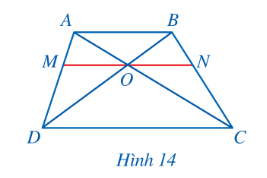
Hướng dẫn giải (SGK – tr,56+57)