CHƯƠNG V: CÁC SỐ ĐẶC TRƯNG CỦA MẪU SỐ LIỆU KHÔNG GHÉP NHÓM

BÀI 14. CÁC SỐ ĐẶC TRƯNG ĐO ĐỘ PHÂN TÁN

1. KHOẢNG BIẾN THIÊN VÀ KHOẢNG TỨ PHÂN VỊ

HĐ1: 

Em đồng ý với nhận định này vì:

Leicester City có điểm lớn nhất là 81 và nhỏ nhất là 41 nên khoảng cách giữa điểm cao nhất và thấp nhất là 40. 

Everton có điểm lớn nhất là 61 và nhỏ nhất là 41 nên khoảng cách giữa điểm cao nhất và thấp nhất là 20. 

Khoảng cách giữa điểm cao nhất và thấp nhất của Everton là ít hơn. 

Kết luận: 

Khoảng biến thiên, kí hiệu là R, là hiệu số giữa giá trị lớn nhất và giá trị nhỏ nhất trong mẫu số liệu. 

Ý nghĩa: 

Khoảng biến thiên dùng để đo độ phân tán của mẫu số liệu. Khoảng biến thiên càng lớn thì mẫu số liệu càng phân tán.

Ví dụ 1 (SGK – tr84)

Luyện tập 1: 

Giá trị nhỏ nhất: 159.

Giá trị lớn nhất: 172.

Khoảng biến thiên: 172 – 159 = 13.

Nhận xét: 

Sử dụng khoảng biến thiên có ưu điểm là đơn giản, dễ tính toán song khoảng biến thiên chỉ sử dụng thông tin của giá trị lớn nhất và giá trị nhỏ nhất mà bỏ qua thông tin từ tất cả các giá trị khác. Do đó, khoảng biến thiên rất dễ bị ảnh hưởng bởi các giá trị bất thường. 

HĐ2: 

a. Hà Nội: 

Khoảng biến thiên là: R$_{1}$ = 35 – 23 = 12

Điện biên: 

Khoảng biến thiên là: R$_{2}$ = 28 – 16 = 12

b. Giá trị 16 làm khoảng biên thiên lớn hơn. 

c. 

• Hà Nội:

- Sắp xếp theo thứ tự không giảm: 23; 25; 28; 32; 33; 35

- Tứ phân vị là: Q$_{2}$ = 28; Q$_{1}$ = 25; Q$_{3}$ = 33. Ta có: Q$_{3}$ – Q$_{1}$ = 33 – 25 = 8. 

• Điện Biên:

- Sắp xếp theo thứ tự không giảm: 16; 24; 26; 26; 26; 27; 28. 

- Tứ phân vị là: Q$_{1}$ = 24; Q$_{2}$ = 26; Q$_{3}$ = 27. Ta có: Q$_{3}$ – Q$_{1}$ = 27 – 24 = 3.

Có thể dùng số liệu này để đo độ phân tán của số liệu. 

Kết luận:

Khoảng tứ phân vị, kí hiệu là ∆Q, là hiệu số giữa tứ phân vị thứ ba và tứ phân vị thứ nhất, tức là: 

 ∆Q=Q$_{3}$- Q$_{1}$

Ý nghĩa: 

Khoảng tứ phân vị cũng là một số đo độ phân tán của mẫu số liệu. Khoảng tứ phân vị càng lớn thì mẫu số liệu càng phân tán. 

Chú ý: 

Một số tài liệu gọi khoảng biến thiên là biên độ và khoảng tứ phân vị là độ trải giữa. 

Ví dụ 2 (SGK – tr85) 

Luyện tập 2: 

Sắp xếp lại mẫu số liệu theo thứ tự không giảm: 

7; 9; 9; 10; 10; 10; 11; 12; 12; 14.

Tứ phân vị là: Q$_{2}$ = 10; Q$_{1}$ = 9; Q$_{3}$ = 12. 

Ta có: Q$_{3}$ – Q$_{1}$ = 12 – 9 = 3

Vậy khoảng tứ phân vị là 3.

2. PHƯƠNG SAI VÀ ĐỘ LỆCH CHUẨN

Kết luận: 

- Phương sai là giá trị s$^{2}$=$\frac{(x_{1}-\bar{x})^{2}+(x_{2}-\bar{x})^{2}+...+(x_{n}-\bar{x})^{2}}{n}$

- Căn bậc hai của phương sai, s=$\sqrt{s^{2}}$, được gọi là độ lệch chuẩn. 

Chú ý:

Người ta còn sử dụng đại lượng để đo độ phân tán của mẫu số liệu: 

s$^{2}$= $\frac{(x_{1}-\bar{x})^{2}+(x_{2}-\bar{x})^{2}+...+(x_{n}-\bar{x})^{2}}{n-1}$

Ý nghĩa: 

Nếu số liệu càng phân tán thì phương sai và độc lệch chuẩn càng lớn. 

Ví dụ 3 (SGK – tr86)

Luyện tập 3: 

Số trung bình của mẫu số liệu là:

$\frac{0,398+0,399+0,408+0,41+0,406+0,405+0,402}{7}$=0,404

Phương sai:

s$^{2}$= $\frac{0,000122}{7}$ ≈0,000017

Vậy độ lệch chuẩn s≈0,0042. Độ chính xác của phép đo cao vì độ lệch chuẩn và phương sai nhỏ.

3. PHÁT HIỆN SỐ LIỆU BẤT THƯỜNG HOẶC KHÔNG CHÍNH XÁC BẰNG BIỂU ĐỒ HỘP

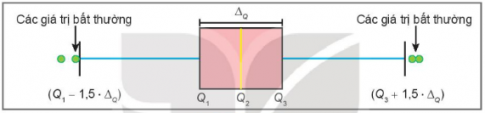
Các giá trị lớn hơn Q$_{3}$+1,5.∆Q hoặc bé hơn Q$_{1}$-1,5.∆Q được xem là giá trị bất thường.

Ví dụ 4 (SGK – tr87) 

Luyện tập 4: 

Ta có Q$_{1}$ = 56; Q$_{3}$ = 84.

Khoảng tứ phân vị:

∆Q=Q$_{3}$- Q$_{1}$=84-56=28.

Do đó,

Q$_{1}$ – 1,5.∆Q = 56 – 1,5.28 = 14

Q$_{3}$ + 1,5.∆Q = 84 – 1,5.28 = 126.

Ta thấy 10 < 14 nên 10 là giá trị bất thường; 14 < 100 < 126 nên 100 không là giá trị bất thường.