CHƯƠNG IX. PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

BÀI 4. BA ĐƯỜNG CONIC TRONG MẶT PHẲNG TỌA ĐỘ

1. ELIP

• Nhận biết elip

HĐKP1:

F$_{1}$M + F$_{2}$M = 2a.

Kết luận:

Cho hai điểm cố định F$_{1}$ , F$_{2}$ và một độ dài không đổi 2a lớn hơn F$_{1}$F$_{2}$. Elip (E) tập hợp các điểm M trong mặt phẳng sao cho F$_{1}$M + F$_{2}$M = 2a.

Các điểm F$_{1}$ và F$_{2}$ gọi là các tiêu điểm của elip.

Độ dài F$_{1}$F$_{2}$  = 2c gọi là tiêu cự của elip (a>c).

• Phương trình chính tắc của elip

HĐKP2

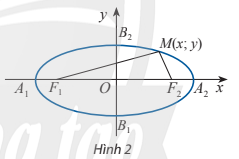
a) F$_{1}$M =$\sqrt{(x_{M}-x_{F_{1}})^{2}+(y_{M}-y_{F_{1}})^{2}}$=$\sqrt{(x+c)^{2}+y^{2}}$

F$_{2}$M = $\sqrt{(x_{M}-x_{F_{2}})^{2}+(y_{M}-y_{F_{2}})^{2}}$=$\sqrt{(x-c)^{2}+y^{2}}$

b) Elip (E) là tập hợp các điểm M trong mặt phẳng sao cho F$_{1}$M + F$_{2}$M = 2a

 $\sqrt{(x+c)^{2}+y^{2}}$+$\sqrt{(x-c)^{2}+y^{2}}$ = 2a.

Kết luận:

M(xy) $\in $ (E) <=> $\frac{x^{2}}{a^{2}}$+$\frac{y^{2}}{b^{2}}$=1

(b=$\sqrt{a^{2}-c^{2}}$,a>b>0)

Trong đó b =$\sqrt{a^{2}-c^{2}}$

Phương trình chính tắc của elip.

* Chú ý:

(E) cắt Ox tại hai điểm A$_{1}$ (-a; 0), A$_{2}$ (a; 0) và cắt Oy tại hai điểm B$_{1}$ (0;-b); B$_{2}$(0; b).

Các điểm A$_{1}$ ; A$_{2}$ ; B$_{1}$ ; B$_{2}$  gọi là các đỉnh của elip.

Đoạn thẳng A$_{1}$A$_{2}$ gọi là trục lớn, đoạn thẳng B$_{1}$B$_{2}$ gọi là trục nhỏ của elip.

Giao điểm O của hai trục gọi là tâm đối xứng của elip.

Nếu M(x; y) (E) thì |x| ≤ a; |y| ≤ b

Ví dụ 1: SGK-tr65

Ví dụ 2: SGK-tr65

Thực hành 1.

Ta có: a = 3; b = 2.

Vậy phương trình chính tắc của (E) là: $\frac{x^{2}}{9}$+$\frac{y^{2}}{4}$ = 1

Vận dụng 1:

Ta có: 2a = 10 a = 5; b = 4.

Vậy phương trình chính tắc của elip (E) là: $\frac{x^{2}}{25}$+$\frac{y^{2}}{16}$ = 1

2. HYPEBOL

• Nhận biết hypebol

HĐKP3:

a) Ta có: MF$_{2}$ + MA = l   MA = l - MF$_{2}$

Lại có MF$_{1}$ + MA = d MF$_{1}$ + l - MF$_{2}$ = d

=> MF$_{1}$ - MF$_{2}$ = d - l = 2a

Vậy MF$_{1}$ - MF$_{2}$ = 2a

b) MF$_{2}$ - MF$_{1}$ = 2a

⇒ Kết luận:

- Cho hai điểm cố định F$_{1}$, F$_{2}$ và một độ dài không đổi 2a nhỏ hơn F$_{1}$F$_{2}$. Hypebol (H) là tập hợp các điểm M trong mặt phẳng sao cho |F$_{1}$M-F$_{2}$M| = 2a

- Các điểm F$_{1}$ và F$_{2}$ gọi là các tiêu điểm của hypebol.

- Độ dài F$_{1}$F$_{2}$ = 2c gọi là tiêu cự của hypebol. (c >a).

HĐKP4:

a) F$_{1}$M =$\sqrt{(x_{M}-x_{F_{1}})^{2}+(y_{M}-y_{F_{1}})^{2}}$=$\sqrt{(x+c)^{2}+y^{2}}$

F$_{2}$M =$\sqrt{(x_{M}-x_{F_{2}})^{2}+(y_{M}-y_{F_{2}})^{2}}$=$\sqrt{(x-c)^{2}+y^{2}}$ 

b) Hypebol (H) là tâp hợp các điểm M trong mặt phẳng sao cho |F$_{1}$M-F$_{2}$M | = 2a

 |$\sqrt{(x+c)^{2}+y^{2}}$-$\sqrt{(x-c)^{2}+y^{2}}$ | = 2a.

⇒ Kết luận:

M(x;y)$\in $ (H) <=> $\frac{x^{2}}{a^{2}}$-$\frac{y^{2}}{b^{2}}$ =1 

Trong đó b=$\sqrt{c^{2}-a^{2}}$

* Chú ý:

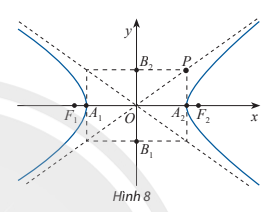
Ví dụ 3: SGK – tr67

Thực hành 2.

Ta có: 2c = 10 => c = 5; 2b = 6 => b = 3

a = $\sqrt{c^{2}-b^{2}}$ =$\sqrt{5^{2}-3^{2}}$ = 4

Vậy phương trình chính tắc của hypebol (H) là: $\frac{x^{2}}{16}$-$\frac{y^{2}}{9}$ = 1

Vận dụng 2.

Theo bài ra ta có, khoảng cách từ nóc tháp đến tâm O bẳng 40m, khoảng cách từ tâm O đến đáy bằng 80m.

Thay y = 40 vào phương trình (H), ta được: 

$\frac{x^{2}}{27^{2}}$-$\frac{40^{2}}{40^{2}}$ = 1

<=>x$^{2}$ = 2. 27$^{2}$ <=>  x =$\pm $ 27$\sqrt{2}$

Bán kính đường tròn nóc bằng 27$\sqrt{2}$ m.

Thay y = 80 vào phương trình (H), ta được: 

$\frac{x^{2}}{27^{2}}$-$\frac{80^{2}}{40^{2}}$ = 1

<=> x$^{2}$= 5. 27$^{2}$ <=>  x = $\pm $27$\sqrt{5}$

Bán kính đường tròn đáy bằng 27$\sqrt{2}$ m.

3. PARABOL

• Nhận biết parabol

HĐKP5

Đồ thị (P) của hàm số (*) vừa tìm được là một parabol.

Phương trình chính tắc của parabol

HĐKP6

a) MF = $\sqrt{(x_{F}-x_{M})^{2}+(y_{F}-y_{M})^{2}}$=$\sqrt{(\frac{p}{2}-)^{2}+(0-y)^{2}}$ = $\sqrt{(\frac{p}{2}-)^{2}+y^{2}}$

d(M, $\Delta $) = |x + $\frac{p}{2}$|

b) Ta có (P) là tập hợp các điểm M cách đều F và nên MF = d(M, $\Delta $)

$\sqrt{(\frac{p}{2}-)^{2}+y^{2}}$ = |x + $\frac{p}{2}$|

Kết luận:

M(xy )∈(P)⇔y$^{2}$=2px 

Phương trình trên được gọi là phương trình chính tắc của parabol.

* Chú  ý: 

+ O gọi là đỉnh của parabil (P)

+ Ox gọi là trục đối xứng của parabol (P)

+ p gọi là tham số tiêu của parabol (P)

+ Nếu M(x; y) ∈ (P) thì x $\geq $ 0 và M'(x; -y) ∈ (P). 

Ví dụ 4: SGK – tr69

Ví dụ 5: SGK – tr69

Thực hành 3.

(P) có đường chuẩn $\Delta $: x + 1 = 0 p = 2

Vậy (P) có phương trình y$^{2}$ = 4x

Vận dụng 3.

Chọ hệ trục tọa độ như hình vẽ. Gọi phương trình của parabol là y$^{2}$ = 2px.

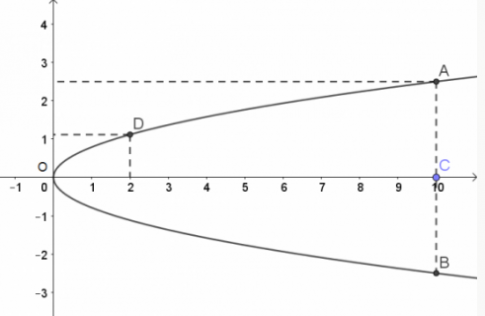
Ta có chiều cao của cổng là OC = 10 m C(10; 0)

Bề rộng của cổng tại chân cổng là AB = 5m => AC = 2,5 m A(10; 2,5)

Vì A(10; 2,5) (P) nên thay tọa độ của A vào phương trình (P), ta được:

2,5$^{2}$ = 2p. 10

p = $\frac{5}{16}$ => (P): y$^{2}$= $\frac{5}{8}$x

Thay tọa độ điểm D(2; a) vào phương trình (P), ta được: 

a$^{2}$= $\frac{5}{8}$. 2 => a = $\frac{\sqrt{5}}{2}$

Vậy bề rộng của cộng tại chỗ cách đỉnh 2m là:

2a = 2. $\frac{\sqrt{5}}{2}$ = $\sqrt{5}$ (m).