Giải bài 3: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
Ở các lớp dưới, chúng ta đã biết được cách tìm GTLN và GTNN của hàm số thông qua một số bất đẳng thức quen thuộc như Bunhiacopski, Cauchy... Bài hôm nay, chúng ta được học thêm một phương pháp nữa để tìm GTLN và GTNN của hàm số đó là nhờ vào một ứng dụng quan trọng của đạo hàm hàm số.
A. Lí thuyết
1. Định nghĩa
Cho hàm số $y=f(x)$ xác định trên tập D.
- Số M được gọi là giá trị lớn nhất của hàm số $y=f(x)$ trên tập D nếu $f(x) \leq M$ với mọi x thuộc D và tồn tại $x_{0} \in D$ sao cho $f(x_{0}=M$. Kí hiệu $M=\max_{D} f(x)$.
- Số m được gọi là giá trị nhỏ nhất của hàm số $y=f(x)$ trên tập D nếu $f(x) \geq m$ với mọi x thuộc D và tồn tại $x_{0} \in D$ sao cho $f(x_{0}=m$. Kí hiệu $m=\min_{D} f(x)$.
2. Cách tính GTLN và GTNN của hàm số trên một đoạn
Định lí: Mọi hàm số liên tục trên một đoạn đều có giá trị lớn nhất và giá trị nhỏ nhất trên đoạn đó.
Quy tắc tìm GTLN và GTNN của hàm số liên tục trên một đoạn
- Tìm các điểm $x_{1}, x_{2},...,x_{n}$ trên khoảng (a,b) tại đó $f'(x)=0$ hoặc $f'(x)$ không xác định.
- Tính $f(a), f(x_{1}), f(x_{2}),..., f(x_{n}),f(b)$.
- Tìm số lớn nhất M và số nhỏ nhất m trong các số trên. Ta có $M=\max_{[a,b]}f(x), m=\min_{[a,b]}f(x)$.
Tổng quát: Muốn tìm GTLN và GTNN của một hàm số trên TXĐ.
- Bước 1: Tìm TXĐ
- Bước 2: Giải phương trình $f'(x)=0$
- Bước 3: Lập bảng biến thiên
- Bước 4: Dựa vào bảng biến thiên đưa ra kết luận.
Ví dụ: Tìm GTLN và GTNN của hàm số $$y=x-5+\frac{1}{x}$$ trên khoảng $(0,+\infty)$.
Giải: TXĐ $D=(0,+\infty)$.
Ta có $y'=1-\frac{1}{x^{2}}=\frac{x^{2}-1}{x^{2}}=0\Leftrightarrow x=1$.
Bảng biến thiên
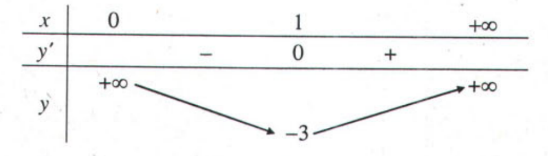
Từ bảng biến thiên ta thấy trên khoảng $(0,+\infty)$, hàm số đạt GTNN là -3 khi x=1 và không tồn tại giá trị lớn nhất của f(x) trên khoảng $(0,+\infty)$.
Giải bài tập những môn khác
Môn học lớp 12 KNTT
5 phút giải toán 12 KNTT
5 phút soạn bài văn 12 KNTT
Văn mẫu 12 KNTT
5 phút giải vật lí 12 KNTT
5 phút giải hoá học 12 KNTT
5 phút giải sinh học 12 KNTT
5 phút giải KTPL 12 KNTT
5 phút giải lịch sử 12 KNTT
5 phút giải địa lí 12 KNTT
5 phút giải CN lâm nghiệp 12 KNTT
5 phút giải CN điện - điện tử 12 KNTT
5 phút giải THUD12 KNTT
5 phút giải KHMT12 KNTT
5 phút giải HĐTN 12 KNTT
5 phút giải ANQP 12 KNTT
Môn học lớp 12 CTST
5 phút giải toán 12 CTST
5 phút soạn bài văn 12 CTST
Văn mẫu 12 CTST
5 phút giải vật lí 12 CTST
5 phút giải hoá học 12 CTST
5 phút giải sinh học 12 CTST
5 phút giải KTPL 12 CTST
5 phút giải lịch sử 12 CTST
5 phút giải địa lí 12 CTST
5 phút giải THUD 12 CTST
5 phút giải KHMT 12 CTST
5 phút giải HĐTN 12 bản 1 CTST
5 phút giải HĐTN 12 bản 2 CTST
Môn học lớp 12 cánh diều
5 phút giải toán 12 CD
5 phút soạn bài văn 12 CD
Văn mẫu 12 CD
5 phút giải vật lí 12 CD
5 phút giải hoá học 12 CD
5 phút giải sinh học 12 CD
5 phút giải KTPL 12 CD
5 phút giải lịch sử 12 CD
5 phút giải địa lí 12 CD
5 phút giải CN lâm nghiệp 12 CD
5 phút giải CN điện - điện tử 12 CD
5 phút giải THUD 12 CD
5 phút giải KHMT 12 CD
5 phút giải HĐTN 12 CD
5 phút giải ANQP 12 CD
Giải chuyên đề học tập lớp 12 kết nối tri thức
Giải chuyên đề Ngữ văn 12 Kết nối tri thức
Giải chuyên đề Toán 12 Kết nối tri thức
Giải chuyên đề Vật lí 12 Kết nối tri thức
Giải chuyên đề Hóa học 12 Kết nối tri thức
Giải chuyên đề Sinh học 12 Kết nối tri thức
Giải chuyên đề Kinh tế pháp luật 12 Kết nối tri thức
Giải chuyên đề Lịch sử 12 Kết nối tri thức
Giải chuyên đề Địa lí 12 Kết nối tri thức
Giải chuyên đề Tin học ứng dụng 12 Kết nối tri thức
Giải chuyên đề Khoa học máy tính 12 Kết nối tri thức
Giải chuyên đề Công nghệ 12 Điện - điện tử Kết nối tri thức
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Kết nối tri thức
Giải chuyên đề học tập lớp 12 chân trời sáng tạo
Giải chuyên đề Ngữ văn 12 Chân trời sáng tạo
Giải chuyên đề Toán 12 Chân trời sáng tạo
Giải chuyên đề Vật lí 12 Chân trời sáng tạo
Giải chuyên đề Hóa học 12 Chân trời sáng tạo
Giải chuyên đề Sinh học 12 Chân trời sáng tạo
Giải chuyên đề Kinh tế pháp luật 12 Chân trời sáng tạo
Giải chuyên đề Lịch sử 12 Chân trời sáng tạo
Giải chuyên đề Địa lí 12 Chân trời sáng tạo
Giải chuyên đề Tin học ứng dụng 12 Chân trời sáng tạo
Giải chuyên đề Khoa học máy tính 12 Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Điện - điện tử Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Chân trời sáng tạo
Giải chuyên đề học tập lớp 12 cánh diều
Giải chuyên đề Ngữ văn 12 Cánh diều
Giải chuyên đề Toán 12 Cánh diều
Giải chuyên đề Vật lí 12 Cánh diều
Giải chuyên đề Hóa học 12 Cánh diều
Giải chuyên đề Sinh học 12 Cánh diều
Giải chuyên đề Kinh tế pháp luật 12 Cánh diều
Giải chuyên đề Lịch sử 12 Cánh diều
Giải chuyên đề Địa lí 12 Cánh diều
Giải chuyên đề Tin học ứng dụng 12 Cánh diều
Giải chuyên đề Khoa học máy tính 12 Cánh diều
Giải chuyên đề Công nghệ 12 Điện - điện tử Cánh diều
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Cánh diều

Bình luận