Slide bài giảng Toán 12 chân trời Bài 3: Đường tiệm cận của đồ thị hàm số
Slide điện tử Bài 3: Đường tiệm cận của đồ thị hàm số. Trình bày với các hiệu ứng hiện đại, hấp dẫn. Giúp học sinh hứng thú học bài. Học nhanh, nhớ lâu. Có tài liệu này, hiệu quả học tập của môn Toán 12 Chân trời sẽ khác biệt
Bạn chưa đủ điều kiện để xem được slide bài này. => Xem slide bài mẫu
Tóm lược nội dung
BÀI 3: ĐƯỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
1. ĐƯỜNG TIỆM CẬN ĐỨNG
Giải hoạt động 1 trang 19 toán 12 tập 1 ctst
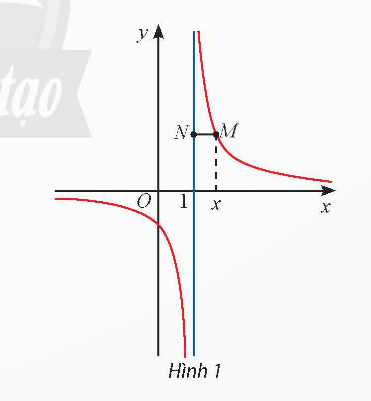
Cho hàm số ![]() có đồ thị như Hình 1.
có đồ thị như Hình 1.
- Tìm
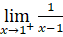 ;
; 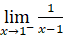
- Gọi M là điểm trên đồ thị có hoành độ x. Đường thẳng đi qua M và vuông góc với trục Oy cắt đường thắng x = 1 tại điểm N. Tính MN theo x và nhận xét về MN khi x
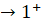 và x
và x 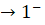 .
.
Trả lời rút gọn:
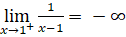 ;
;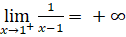
- Ta có tọa độ M(x; y); N(1; y)
![]() Độ dài MN là: MN =
Độ dài MN là: MN = ![]() = x – 1
= x – 1
Khi x ![]() và x
và x ![]() thì độ dài của MN càng giảm, điểm M di chuyển lại gần điểm N hơn.
thì độ dài của MN càng giảm, điểm M di chuyển lại gần điểm N hơn.
Giải thực hành 1 trang 20 toán 12 tập 1 ctst
Tìm tiệm cận đứng của đồ thị của các hàm số sau:
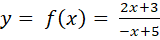 ; b)
; b)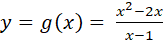
Trả lời rút gọn:
Tập xác định: D = ![]()
Ta có: ![]() ;
;![]() .
.
Suy ra đường thẳng x = 5 là đường tiệm cận đứng của đồ thị f(x).
Tập xác định: D = ![]()
Ta có: ![]() ;
;![]() .
.
Suy ra đường thẳng x = 1 là đường tiệm cận đứng của đồ thị g(x).
2. ĐƯỜNG TIỆM CẬN NGANG:
Giải hoạt động 2 trang 21 toán 12 tập 1 ctst
Cho hàm số ![]() có đồ thị như Hình 4.
có đồ thị như Hình 4.
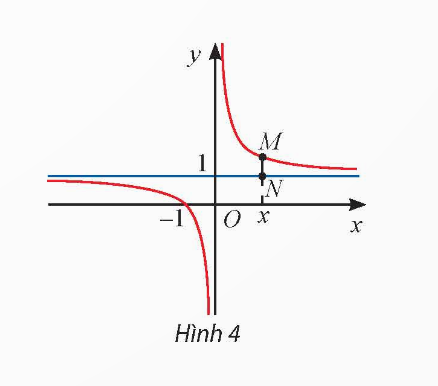
- Tìm
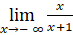 ;
; 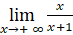
- Đường thẳng vuông góc với trụ Ox tại điểm x cắt đồ thị hàm số tại điểm M và cắt đường thẳng y = 1 tại điểm N (Hình 4). Tính MN theo x và nhận xét về MN khi x
 + ∞ hoặc x
+ ∞ hoặc x  - ∞
- ∞
Trả lời rút gọn:
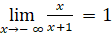 ;
; 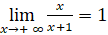
Giải thực hành 2 trang 21 toán 12 tập 1 ctst
Tìm tiệm cận đứng của đồ thị của các hàm số sau:
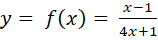 ; b)
; b)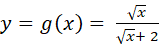
Trả lời rút gọn:
- Tập xác định: D =
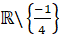
Ta có: ![]()
![]()
Vậy đường thẳng y = ![]() là tiệm cận ngang của đồ thị hàm số.
là tiệm cận ngang của đồ thị hàm số.
- Tập xác định: D = [0; + ∞)
Ta có:![]()
Vậy đường thẳng y = 1 là tiệm cận ngang của đồ thị hàm số.
3. ĐƯỜNG TIỆM CẬN XIÊN:
Giải hoạt động 3 trang 22 toán 12 tập 1 ctst
Cho đồ thị của hàm số ![]() và đường thẳng
và đường thẳng ![]() . Đường thẳng vuông góc với trục Ox tại điểm x cắt đồ thị hàm số tại điểm M và cắt đường thẳng
. Đường thẳng vuông góc với trục Ox tại điểm x cắt đồ thị hàm số tại điểm M và cắt đường thẳng ![]() tại điểm N (Hình 7).
tại điểm N (Hình 7).
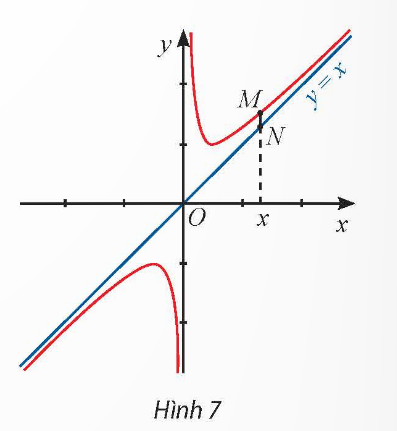
- Tìm
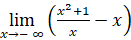 ;
; 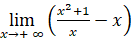
- Tính MN theo x và nhận xét về MN khi x
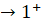 và x
và x 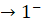 .
.
Trả lời rút gọn:
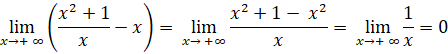
Giải thực hành 3 trang 24 toán 12 tập 1 ctst
Tìm tiệm cận xiên của đồ thị hàm số ![]() .
.
Trả lời rút gọn:
![]()
Tập xác định: D =![]()
Ta có: ![]()
![]()
Ta cũng có: ![]() ;
; ![]()
Đồ thị có tiệm cận xiên là đường thẳng ![]()
Giải thực hành 4 trang 24 toán 12 tập 1 ctst
Nếu trong một ngày, một xưởng sản xuất được x kilogam sản phẩm thì chi phí trung bình (tính bằng nghìn đồng) cho một sản phẩm được cho bởi công thức:
![]()
Tìm các đường tiệm cận của đồ thị hàm số ![]()
Trả lời rút gọn:
Tập xác định: D = ![]()
- Ta có:
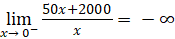 ;
;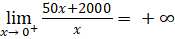 .
.
Vậy đường thẳng x = 0 hay trục tung là đường tiệm cận đứng của đồ thị ![]()
- Ta có:
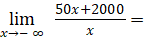
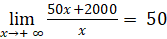
Vậy đường thẳng y = 50 là tiệm cận ngang của đồ thị hàm số.
- Ta có:
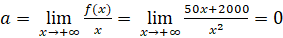
![]() = 50
= 50
Đồ thị không có tiệm cận xiên.
Vậy đồ hàm số ![]() có đường thẳng x = 0 hay trục tung là đường tiệm cận đứng và đường thẳng y = 50 là tiệm cận ngang.
có đường thẳng x = 0 hay trục tung là đường tiệm cận đứng và đường thẳng y = 50 là tiệm cận ngang.
4. GIẢI BÀI TẬP CUỐI SÁCH GIÁO KHOA
Giải bài 1 trang 24 toán 12 tập 1 ctst
Tìm các tiệm cận đứng và tiệm cận ngang của đồ thị hàm số sau:
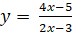 ; b)
; b) 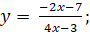 c)
c) 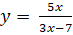
Trả lời rút gọn:
Tập xác định: D =
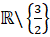
- Ta có:
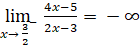 ;
;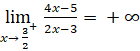 .
.
Suy ra đường thẳng x = ![]() là đường tiệm cận đứng của đồ thị.
là đường tiệm cận đứng của đồ thị.
- Ta có:
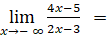
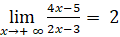
Vậy đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số.
Tập xác định: D =
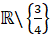
- Ta có:
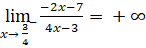 ;
;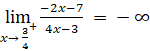 .
.
Suy ra đường thẳng x = ![]() là đường tiệm cận đứng của đồ thị.
là đường tiệm cận đứng của đồ thị.
- Ta có:
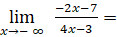
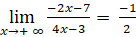
Vậy đường thẳng y = ![]() là tiệm cận ngang của đồ thị hàm số.
là tiệm cận ngang của đồ thị hàm số.
Tập xác định: D =
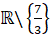
- Ta có:
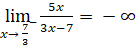 ;
;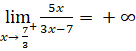 .
.
Suy ra đường thẳng x = ![]() là đường tiệm cận đứng của đồ thị.
là đường tiệm cận đứng của đồ thị.
- Ta có:
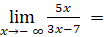
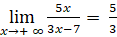
Vậy đường thẳng y = ![]() là tiệm cận ngang của đồ thị hàm số.
là tiệm cận ngang của đồ thị hàm số.
Giải bài 2 trang 24 toán 12 tập 1 ctst
Tìm các tiệm cận đứng và tiệm cận xiên của đồ thị hàm số sau:
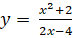 ; b)
; b) 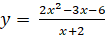 ; c)
; c)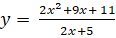
Trả lời rút gọn:
Tập xác định: D =
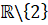
Ta có:
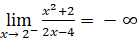 ;
;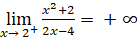 .
.
Suy ra đường thẳng x = 2 là đường tiệm cận đứng của đồ thị.
- Ta có:
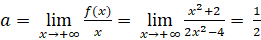
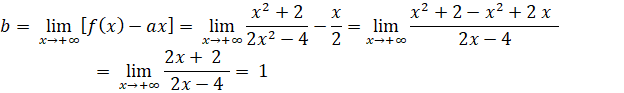
Ta cũng có: ![]() ;
; ![]()
Đồ thị có tiệm cận xiên là đường thẳng ![]()
Tập xác định: D =
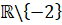
Ta có:
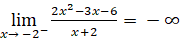 ;
;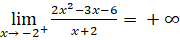 .
.
Suy ra đường thẳng x = -2 là đường tiệm cận đứng của đồ thị.
- Ta có:
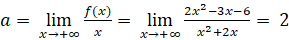
![]()
Ta cũng có: ![]() ;
; ![]()
Đồ thị có tiệm cận xiên là đường thẳng ![]()
Tập xác định: D =
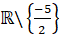
- Ta có:
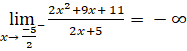 ;
;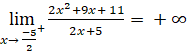 .
.
Suy ra đường thẳng x = ![]() là đường tiệm cận đứng của đồ thị.
là đường tiệm cận đứng của đồ thị.
- Ta có:
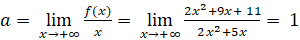
![]()
Ta cũng có: ![]() ;
; ![]()
Đồ thị có tiệm cận xiên là đường thẳng ![]()
Giải bài 3 trang 24 toán 12 tập 1 ctst
Tìm các tiệm cận của đồ thị hàm số sau:
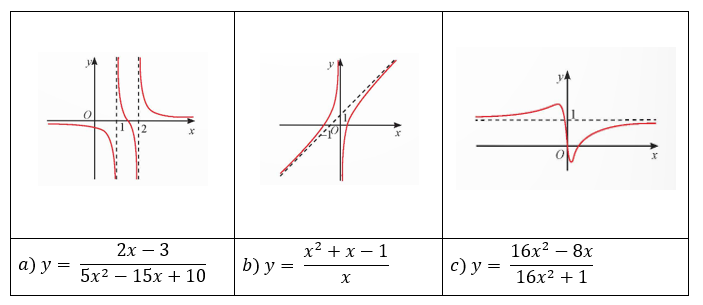
Trả lời rút gọn:
Tập xác định: D =
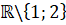
Ta có:
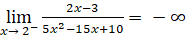 ;
;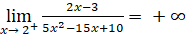 . Suy ra đường thẳng x = 2 là đường tiệm cận đứng của đồ thị.
. Suy ra đường thẳng x = 2 là đường tiệm cận đứng của đồ thị.
![]() ;
;![]() . Suy ra đường thẳng x = 1 là đường tiệm cận đứng của đồ thị.
. Suy ra đường thẳng x = 1 là đường tiệm cận đứng của đồ thị.
Ta có:
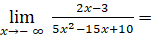
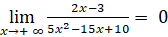
Suy ra đường thẳng y = 0 hay trục hoành là tiệm cận ngang của đồ thị hàm số.
Tập xác định: D =
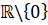
Ta có:
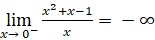 ;
;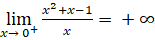 . Suy ra đường thẳng x = 0 hay trục tung là đường tiệm cận đứng của đồ thị.
. Suy ra đường thẳng x = 0 hay trục tung là đường tiệm cận đứng của đồ thị.Ta có:
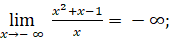
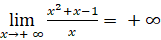
Vậy đồ thị không có đường tiệm cận ngang.
- Ta có:
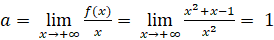
![]()
Ta cũng có: ![]() ;
; ![]()
Đồ thị có tiệm cận xiên là đường thẳng ![]()
- Tập xác định: D =
Đồ thị không có đường tiệm cận đứng.
Ta có:
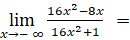
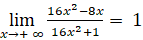
Suy ra đường thẳng y = 1là tiệm cận ngang của đồ thị hàm số.
Giải bài 4 trang 25 toán 12 tập 1 ctst
Nồng độ oxygen trong hồ theo thời gian t cho bởi công thức ![]() với
với ![]() được tính theo
được tính theo ![]() và
và ![]() được tính theo giờ,
được tính theo giờ, ![]() . Tìm các đường tiệm cận của đồ thị hàm số
. Tìm các đường tiệm cận của đồ thị hàm số ![]() . Từ đó, có nhận xét gì về nồng độ oxygen trong hồ khi thời gian
. Từ đó, có nhận xét gì về nồng độ oxygen trong hồ khi thời gian ![]() trở nên rất lớn?
trở nên rất lớn?
Trả lời rút gọn:
![]()
Tập xác định: D = ![]()
Đồ thị không có đường tiệm cận đứng.
Ta có: ![]() . Suy ra đường thẳng y = 5 là đường tiệm cận ngang của đồ thị hàm số.
. Suy ra đường thẳng y = 5 là đường tiệm cận ngang của đồ thị hàm số.
Đồ thị không có đường tiệm cận xiên.
Nhận xét: Nồng độ oxygen trong hồ sẽ gần đạt tới 5![]() khi thời gian
khi thời gian ![]() trở nên rất lớn.
trở nên rất lớn.
