Một con lắc đơn gồm sợi dây có chiều dài 1,20 m và vật có khối lượng 0,500 kg. Treo con lắc tại nơi có gia tốc trọng trường 9.81 m/s$^{2}$. Kéo vật ra khỏi vị trí cân bằng sao cho sợi dây tạo với phương thẳng đứng một góc...

a) Khi góc $\alpha_{0} = 8 ,00^{o} =0,140$ rad con lắc dao động với biên độ nhỏ nên được coi là dao động điều hoà với tần số góc: $\omega = \sqrt\frac{g}{l} = 2, 86 rad / s$

Biên độ của con lắc: $A=l. \alpha_{0} = 0 ,168 m$. 

Tốc độ của vật khi qua vị trí cân bằng O: v=\omega A=0,480 m/s$

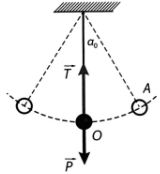
Ở vị trí cân bằng, tổng hợp trọng lực và lực căng dây treo tác dụng lên vật đóng vai trò là lực hướng tâm:

$T - P =F_{ht} = \frac{mv^{2}_{max}}{l}\Rightarrow T=P+ \frac{mv^{2}_{max}}{l}$

Thay số:

T = 5,00N

b) Khi góc $\alpha_{0} = 30,0^{o}$ dao động của con lắc đơn không phải là dao động điều hoà. Chọn gốc thế năng hấp dẫn tại điểm O, áp dụng định luật bảo toàn cơ năng cho chuyển động của con lắc đơn ở môi trường không có lực cản.

$W_{o}=W_{A} \Leftrightarrow \frac{1}{2}mv^{2}_{max} =mgl(l-cos\alpha_{0})$

$\Leftrightarrow v_{max} = \sqrt{2gl(l-cos \alpha_{0})} =1,78 m/s $

Lực căng dây: $T=P+ \frac{mv^{2}_{max}}{l}$

Thay số: T = 6,23N