Hai đường thẳng AB và CD cắt nhau tại O. Cho Om là tia phân giác của góc BOD và$ \widehat{BOM}=30^{\circ}$. Số đo của góc AOC bằng:
5. Hai đường thẳng AB và CD cắt nhau tại O. Cho Om là tia phân giác của góc BOD và$ \widehat{BOM}=30^{\circ}$. Số đo của góc AOC bằng:
A. $30^{\circ}$;
B. $60^{\circ}$;
C. $120^{\circ}$;
D. Một kết quả khác.
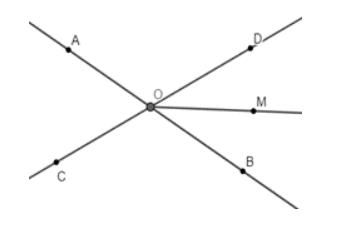
Vì Om là tia phân giác của góc BOD nên $\widehat{BOM}=\widehat{MOD}=\frac{\widehat{BOD}}{2}=30^{\circ}$.
Suy ra $\widehat{BOD}=2 \times 30^{\circ}=60^{\circ}$.
Lại có, $\widehat{BOD}$ và $\widehat{AOC}$ là hai góc đối đỉnh nên $\widehat{BOD}=\widehat{AOC}=60^{\circ}$.
Đáp án: B
Xem toàn bộ: Giải SBT toán 7 Kết nối tri thức Ôn tập chương III
Giải những bài tập khác
Giải bài tập những môn khác
Giải sgk lớp 7 cánh diều
Giải SBT lớp 7 kết nối tri thức
Giải SBT lớp 7 chân trời sáng tạo
Giải SBT lớp 7 cánh diều
Trắc nghiệm 7 Kết nối tri thức
Trắc nghiệm 7 Chân trời sáng tạo
Trắc nghiệm 7 Cánh diêu
Bình luận