Gọi M và N lần lượt là trung điểm các đoạn thẳng cạnh BC và EF của hai tam giác ABC và DEF.
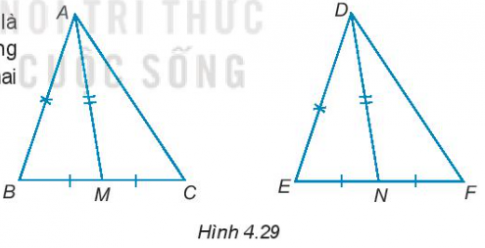
4.29. Gọi M và N lần lượt là trung điểm các đoạn thẳng cạnh BC và EF của hai tam giác ABC và DEF. Giả sử rằng AB = DE, BC = EF, AM = DN (H.4.29). Chứng minh rằng $\Delta ABC = \Delta DEF.$
Vì M là trung điểm của BC nên BM = MC = $\frac{BC}{2}$
Vì N là trung điểm của EF nên EN = NF = $\frac{EF}{2}$
Mà BC = EF (giả thiết) nên BM = EN.
Xét $\Delta ABM$ và $\Delta DEN$ ta có:
AB = DE (giả thiết)
BM = EN (chứng minh trên)
AM = DN (giả thiết)
Do đó, $\Delta ABM = \Delta DEN$ (c . c . c).
Suy ra, $\widehat{ABM}=\widehat{DEN}$ (hai góc tương ứng) hay $\widehat{ABC}=\widehat{DEF}$.
Xét $\Delta ABC$ và $\Delta DEF$ ta có:
AB = DE (giả thiết)
BC = EF (giả thiết)
$\widehat{ABC}=\widehat{DEF}$ (chứng minh trên)
Do đó, $\Delta ABC = \Delta DEF$ (c . g . c).

Bình luận