Giải sbt toán 6 tập 2: bài tập 117 trang 32

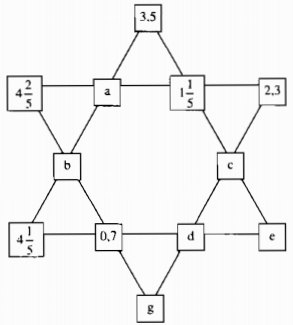
Ta có

• \(4{2 \over 5} + a + 1{1 \over 5} + 2,3 = 8,3\)

\(\left( {4{2 \over 5} + 1{1 \over 5}} \right) + a = 6 \)

\(5{3 \over 5} + a = 6 \)

\(a = 6 - 5{3 \over 5} \)

\(a= 5{5 \over 5} - 5{3 \over 5} \)

\(a= {2 \over 5} \)

• \(3,5 + a + b + 4{1 \over 5} = 8,3 \)

\(3,5 + \left( {{2 \over 5} + 4{1 \over 5}} \right) + b = 8,3 \)

\(4{3 \over 5} + b = 8,3 - 3,5 \)

\(4,6 + b = 4,8 \)

\(b = 4,8-4,6=0,2 \)

• \(4{2 \over 5} + b + 0,7 + g = 8,3 \)

\(\left( {4,4 + 0,2 + 0,7} \right) + g = 8,3 \)

\(5,3 + g = 8,3 \)

\(g = 8,3 - 5,3 = 3\)

• \(3,5 + 1,2 + c + e = 8,3 \)

\(c + e = 8,3 - 4,7 = 3,6\,\,\,(1)\)

• \(4,2 + 0,7 + d + e = 8,3 \)

\(d + e = 8,3 - 4,9 = 3,4\,\,\,(2)\)

• \(2,3 + 3 + d + c = 8,3 \)

\(c + d = 8,3 - 5,3 = 3\,\,\,(3)\)

Cộng từng vế (1), (2) và (3):

\(2 (c + d + e) = 3, 6 + 3, 4 + 3\)

\(2(c + d + e) =10\)

\(c+d+e=5\)

\(\Rightarrow d = 1, 4;  c = 1, 6; e = 2\)

Vậy $a=\frac{2}{5}; b= \frac{1}{5}; c=1,6; d=1,4; e=2; g=3$