Giải hoạt động 3 trang 8 chuyên đề toán 10 kết nối
Hoạt động 3. Giải hệ phương trình bậc nhất ba ẩn bằng phương pháp Gauss
Cho hệ phương trình
a, Khử ẩn x của phương trình thứ hai bằng cách cộng phương trình này với phương trình thứ nhất theo từng vế tương ứng. Viết phương trình nhận được( phương trình này không còn chứa ẩn x và là phương trình thứ hau của hệ mới, tương đương với hệ ban đầu)
b, Khử ẩn của phương trình thứ ba bằng cách nhân phương trình thứ nhất với -2 rồi cộng với phương trình thứ ba theo từng vế tương ứng. Viết phương trình thứ ba mới nhận được. Từ đó viết hệ mới nhận được sau hai bước trên( đã khử x ở hai phương trình cuối)
c, Làm tương tự đối với hệ mới nhận được ở câu b), từ phương trình thứ 2 và thứ ba khử ẩn y ở phương trình thứ ba. Viết hệ dang tam giác nhận được.
d, Giải hệ dạng tam giác nhận được ở câu c). Từ đó suy ra nghiệm của hệ đã cho.
a, Cộng phương trình thứ hai với phương trình thứ nhất , ta được:
b, Nhân phương trình thứ nhất với -2 và cộng với phương trình thứ ba, ta được:
⇔ –y – 5z = –11
⇔ y + 5z = 11.
Hệ mới nhận được sau hai bước trên là :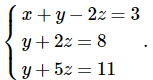 
c, Lấy phương trình thứ hai rừ phương trình thứ ba, ta được:
(y + 2z) – (y + 5z) = 8 – 11
⇔ –3z = –3 ⇔ z = 1.
Hệ tam giác nhận được là: 
d, Ta có:
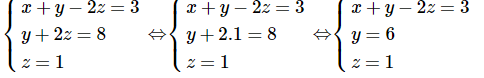
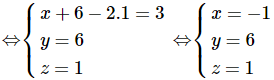
Vậy nghiệm của hệ đã cho là ( x;y;z) = (-1;6;1)
Giải những bài tập khác
Giải bài tập những môn khác
Giải SGK 10 KNTT
Giải SGK 10 CTST
Giải SGK 10 Cánh diều
Giải SBT lớp 10 kết nối tri thức
Giải SBT lớp 10 chân trời sáng tạo
Giải SBT lớp 10 Cánh diều
Giải chuyên đề học tập 10 Kết nối tri thức
Giải chuyên đề học tập 10 Chân trời sáng tạo
Giải chuyên đề học tập 10 Cánh diều
Trắc nghiệm 10 Kết nối tri thức
Trắc nghiệm 10 Chân trời sáng tạo
Trắc nghiệm 10 Cánh diều
Bình luận