Giải câu 97 Bài: Ôn tập chương 3 sgk Toán 9 tập 2 Trang 105

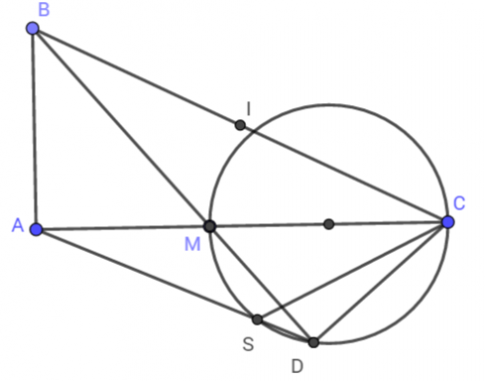
a) Ta có: $\widehat{MDC}=90^{\circ}$ (góc nội tiếp chắn nửa đường tròn)

=> $\widehat{BDC}=90^{\circ}$

=> Điểm D nhìn cạnh BC dưới 1 góc vuông. (1)

mặt khác: $\widehat{BAC}=90^{\circ}$  (tam giác ABC vuông tại A - gt)

=> Điểm A nhìn cạnh BC dưới 1 góc vuông. (2)

Từ (1)(2) => Tứ giác ABCD nội tiếp đường tròn đường kính BC.

b) $\widehat{ABD}$ và $\widehat{ACD}$ là hai góc nội tiếp cùng chắn cung AD của đường tròn đường kính BC

=> $\widehat{ABD}=\widehat{ACD}$ (đpcm)

c) Xét đường tròn đường kính MC, ta có: $\widehat{SDM}=\widehat{MCS}$ (hai góc nội tiếp cùng chắn cung MD)  (3)

Xét đường tròn đường kính BC, ta có: $\widehat{SDM}=\widehat{BCA}$ (hai góc nội tiếp cùng chắn cung AB)     (4)

Từ (3)(4) => $\widehat{MSC}=\widehat{BCA}$  ($=\widehat{SDM}$)

CA là tia phân giác $\widehat{SCB}$  (đpcm)