Giải câu 95 Bài: Ôn tập chương 3 sgk Toán 9 tập 2 Trang 105

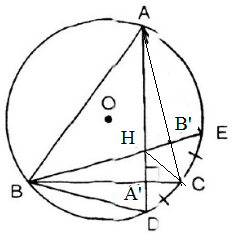
Gọi giao của các đường cao hạ từ A và B với AC, BC lần lượt là: B', A'.

a) Vì AD vuông góc BC nên $\widehat{AA'B}=90^{\circ}$ mà $\widehat{AA'B}$ là góc có đỉnh nằm trong (O)

=> $\widehat{AA'B}=\frac{1}{2}$. (sđ cung AB + sđ cung CD)

=> sđ cung AB + sđ cung CD = $2.90^{\circ}=180^{\circ}$  (1)

Tương tự, BE vuông góc AC => $\widehat{AABB}=90^{\circ}$ mà $\widehat{AB'B}$ là góc có đỉnh nằm trong (O)

=> $\widehat{AB'B}=\frac{1}{2}$. (sđ cung AB + sđ cung CE)

=> sđ cung AB + sđ cung CE = $2.90^{\circ}=180^{\circ}$  (2)

Từ (1)(2) => sđ cung CD = sđ cung CE

=> CD = CE (trong 1 đường tròn, 2 cung bằng nhau căng hai dây bằng nhau)

b) Ta có: sđ cung CD = sđ cung CE (cmt)

=> $\widehat{EBC}=\widehat{CBD}$ (hai góc nội tiếp chắn hai cung bằng nhau trong 1 đường tròn)

Xét tam giác BHD có: BA' là đường phân giác (do $\widehat{HBA'}=\widehat{A'BD}$ - cmt) đồng thời BA' là đường cao (do BC vuông góc AD)

nên tam giác BHD là tam giác cân đỉnh B (dấu hiệu nhận biết) (đpcm)

c) Tam giác BHD là tam giác cân đỉnh B (cmt)

=> BA' đồng thời là đường trung trực của đoạn HD 

=> BC là trung trực của HD

=> CH = CD (tính chất đường trung trực của đoạn thẳng)