Giải câu 6 bài phương trình đường tròn
Bài tập 6. Hình 46 mô phỏng một trạm thu phát sóng điện thoại di động đặt ở vị trí I có toạ độ (– 2 ; 1) trong mặt phẳng toạ độ (đơn vị trên hai trục là ki-lô-mét).
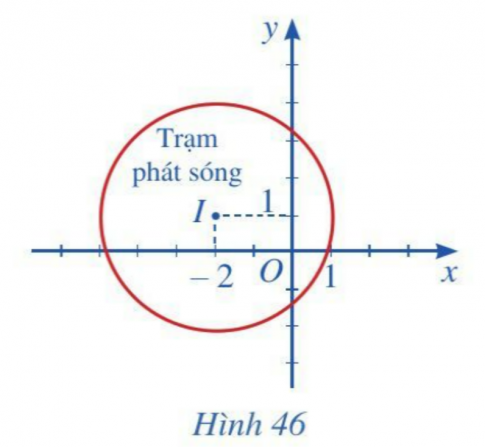
a. Lập phương trình đường tròn mô tả ranh giới bên ngoài của vùng phủ sóng, biết rằng trạm thu phát sóng đó được thiết kế với bán kính phủ sóng 3 km.
b. Nếu người dùng điện thoại ở vị trí có toạ độ (− 1 ; 3) thì có thể sử dụng dịch vụ của trạm này không? Giải thích.
c. Tính theo đường chim bay, xác định khoảng cách ngắn nhất để một người ở vị trí có toạ độ (– 3 ; 4) di chuyển được tới vùng phủ sóng theo đơn vị ki-lô-mét (làm tròn kết quả đến hàng phần mười).
a. Đường tròn mô tả ranh giới bên ngoài của vùng phủ sóng đi qua tâm I(-2;1), có bán kính phủ sóng 3km nên phương trình đường tròn đó là:
${{\left( x+2 \right)}^{2}}+{{\left( y-1 \right)}^{2}}=9$
b. Nếu người dùng điện thoại ở vị trí có tọa độ M (-1;3)
$\Rightarrow IM=\sqrt{{{\left( -1-(-2) \right)}^{2}}+{{\left( 3-1 \right)}^{2}}}=\sqrt{13}\approx 3,6>R$
$\Rightarrow $ Người dùng điện thoại ở vị trí có tọa độ (-1;3) không thể sử dụng dịch vụ của trạm này.
c.

Giả sử vị trí đứng của người đó là B(-3;4).
(BI) qua I (-2;1), nhận vecto pháp tuyến $\overrightarrow{{{n}_{BI}}}\bot \overrightarrow{BI}(1;-3)\Rightarrow \overrightarrow{{{n}_{BI}}}(3;1)$
$\Rightarrow$ Phương trình tổng quát của (BI): 3(x+2)+1(y-1) = 0
hay (BI): 3x+y+5=0
Gọi A là giao điểm của đường tròn tâm I và (BI)
$\Rightarrow$ Khoảng cách ngắn nhất để người đó di chuyển được từ vị trí B(-3; 4) tới vùng phủ sóng là BI.
Tọa độ của A là nghiệm của hệ
$\left\{ \begin{align}& 3x+y+5=0 \\& {{\left( x+2 \right)}^{2}}+{{\left( y-1 \right)}^{2}}=9 \\\end{align} \right.$
$\Leftrightarrow \left\{ \begin{align}& y=-3x-5 \\& {{(x+2)}^{2}}+{{(-3x-5-1)}^{2}}=9 \\\end{align}\right.$ $\Leftrightarrow \left\{ \begin{align}& y=-3x-5 \\ & {{(x+2)}^{2}}+{{(-3x-6)}^{2}}=9 \\\end{align} \right.$
$\Leftrightarrow \left\{ \begin{align}& y=-3x-5 \\& {{(x+2)}^{2}}+9{{(x+2)}^{2}}=9 \\\end{align} \right.$ $\Leftrightarrow \left\{ \begin{align}& y=-3x-5 \\ & {{(x+2)}^{2}}=\frac{9}{10} \\\end{align} \right.$
$\Leftrightarrow \left\{ \begin{align}& y=-3x-5 \\& x+2=\frac{-3\sqrt{10}}{10} \\\end{align} \right.$
$\Leftrightarrow \left\{ \begin{align}& y=\frac{10+9\sqrt{10}}{10} \\& x=-\frac{20+3\sqrt{10}}{10} \\\end{align} \right.$
$\Rightarrow AB=\sqrt{{{\left( -\frac{20+3\sqrt{10}}{10}+2 \right)}^{2}}+{{\left( \frac{10+9\sqrt{10}}{10}-1 \right)}^{2}}}=3$
Xem toàn bộ: Giải bài 5 Phương trình đường tròn

Bình luận