Giải câu 3 bài 4: Bất phương trình bậc nhất hai ẩn sgk Đại số 10 trang 99
Câu 3: trang 99 sgk Đại số 10
Có ba nhóm máy \(A, B, C\) dùng để sản xuất ra hai loại sản phẩm I và II. Để sản xuất một đơn vị sản phẩm mỗi loại phải lần lượt dùng các máy thuộc các nhóm khác nhau. Số máy trong một nhóm và số máy của từng nhóm cần thiết để sản xuất ra một đơn vị sản phẩm thuộc mỗi loại được cho trong bảng sau:
| Nhóm | Số máy trong mỗi nhóm | Số máy trong từng nhóm để sản xuất ra một đơn vị sản phẩm | |
| Loại I | Loại II | ||
| A | 10 | 2 | 2 |
| B | 4 | 0 | 2 |
| C | 12 | 2 | 4 |
Một đơn vị sản phẩm I lãi \(3\) nghìn đồng, một sản phẩm II lãi \(5\) nghìn đồng. Hãy lập phương án để việc sản xuất hai loại sản phẩm trên có lãi cao nhất.
Hướng dẫn: Áp dụng phương pháp giải trong mục IV
Gọi \(x\) là số đơn vị sản phẩm loại I, \(y\) là số đơn vị sản phẩm loại II được nhà máy lập kế hoạch sản xuất.
Khi đó số lãi nhà máy nhân được là \(P = 3x + 5y\)(nghìn đồng).
Các đại lượng \(x, y\) phải thỏa mãn các điều kiện sau:
\(\left\{\begin{matrix}x\geq 0 & \\ y\geq 0 & \\ 2x+2y\leq 10 & \\ 2y\leq 4 & \\ 2x+4y\leq 12 & \end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix}x\geq 0 & \\ y\geq 0 & \\ x+y\leq 5 & \\ y\leq 2 & \\ x+2y\leq 6 & \end{matrix}\right.\)
Ta vẽ 5 đường thắng \(x=0; y=0; x+y-5=0; y=2; x+2y-6=0\)
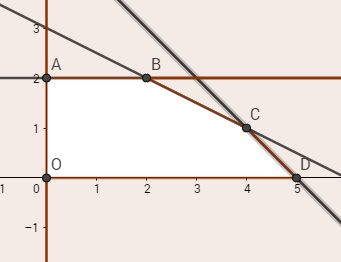
Miền nghiệm của hệ bất phương trình là đa giác \(OABCD\)(kể cả biên).
- Biểu thức \(3x+5y\)có giá trị 10 tại đỉnh \(A(0;2)\)
- Biểu thức \(3x+5y\)có giá trị 16 tại đỉnh \(B(2;-2)\)
- Biểu thức \(3x+5y\)có giá trị 17 tại đỉnh \(C(4;1)\)
- Biểu thức \(3x+5y\)có giá trị 15 tại đỉnh \(D(5;0)\)
Biểu thức \(F = 3x + 5y\)đạt giá trị lớn nhất khi \((x; y)\) là tọa độ đỉnh \(C\).
Vậy để có tiền lãi cao nhất, mỗi ngày cần sản xuất 4 đơn vị sản phầm loại I và 1 đơn vị loại II.

Bình luận