Giải bài tập 1.6 trang 14 chuyên đề toán 10 kết nối
1.6. Cho hệ phương trình bậc nhất ba ẩn sau:
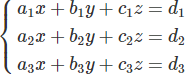
a, Giả sử (Xo;Yo;Zo) Và (X1;Y1;Z1) là hai nghiệm phân biệt của hệ phương trình trên. Chứng minh rằng ![]()
b, Sử dụng kết quả của câu a, Chứng minh rằng, nếu hệ phương trình bậc nhất ba ẩn có hai nghiệm phân biệt thì nó sẽ có vô số nghiệm.
a, Vì (Xo;Yo;Zo) Và (X1;Y1;Z1) là hai nghiệm phân biệt của hệ phương trình trên nên:

Mặt khác do (Xo;Yo;Zo) Và (X1;Y1;Z1) phân biệt nên ![]() cũng đôi một phân biệt với (Xo;Yo;Zo) Và (X1;Y1;Z1).
cũng đôi một phân biệt với (Xo;Yo;Zo) Và (X1;Y1;Z1).
Do đó: ![]() cũng là một nghiệm của hệ.
cũng là một nghiệm của hệ.
b, Xét hệ phương trình bậc nhất ba ẩn 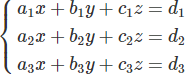
Ta có : (Xo;Yo;Zo) Và (X1;Y1;Z1) là hai nghiệm phân biệt của hệ phương trình này.
Giả sử hệ chỉ có n nghiệm đôi một phân biệt (Xo;Yo;Zo), (X1;Y1;Z1),....(Xn;Yn;Zn)
Ta chọn ra hai nghiệm (Xi;Yi;Zi)., và (Xj;Yj;Zj) thỏa mãn Xj và Yj là hai số nhỏ nhất trong tập hợp A=(Xo;X1;...Xn)
Sau đó áp dụng câu a vào ta được ![]() cũng là một nghiệm của hệ phương trình.
cũng là một nghiệm của hệ phương trình.
Mặt khác (Xi+Xj)/2 khác Xi; Xj và ![]() < Max( Xi;Xj) nên
< Max( Xi;Xj) nên ![]() không trùng với phần tử nào trong tập hợp A. Do đó hệ đã cho có n+1 nghiệm phân biệt => Điều này vô lí.
không trùng với phần tử nào trong tập hợp A. Do đó hệ đã cho có n+1 nghiệm phân biệt => Điều này vô lí.
Vậy hệ này có vô số nghiệm.

Bình luận