Giải bài 5 trang 94 SBT toán 10 tập 1 chân trời
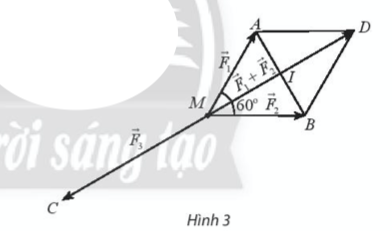
Bài 5 : Cho ba lực $\overrightarrow{F1}$ = $\overrightarrow{MA}$ , $\overrightarrow{F2}$ = $\overrightarrow{MB}$ , $\overrightarrow{F3}$ = $\overrightarrow{MC}$ cùng tác động vào một vật tại điểm M và vật đứng yên. Cho biết độ lớn của $\overrightarrow{F1}$ , $\overrightarrow{F2}$ đều là 100 N và góc AMB = 60°. Tìm độ lớn của lực $\overrightarrow{F3}$.
M đứng yên nên $\overrightarrow{F1}$ + $\overrightarrow{F2}$ + $\overrightarrow{F3}$ = $\overrightarrow{0}$ suy ra $\overrightarrow{F3}$ = -($\overrightarrow{F1}$ + $\overrightarrow{F2}$)
Ta cần tính $\overrightarrow{F1}$ + $\overrightarrow{F2}$ .
Cường độ $\overrightarrow{F1}$ và $\overrightarrow{F2}$ đều là 100 N.
=> |$\overrightarrow{F1}$| = |$\overrightarrow{F2}$| = 100.
Dựng hình bình hành MADB.
Gọi I là giao điểm của AB và MD, khi đó I là trung điểm của AB và MD.
Mặt khác góc AMB = 60° nên ∆ABM đều.
Khi đó MI ⊥ AB => ∆AIM vuông tại I.
=> MI = AMsin(MAI)^ = 100 . sin60° = 50√3 = 100√3 .
Mà $\overrightarrow{F3}$ = -($\overrightarrow{F1}$ + $\overrightarrow{F2}$) = -($\overrightarrow{MA}$ + $\overrightarrow{MB}$) = - $\overrightarrow{MD}$.
Do đó $\overrightarrow{F3}$ có hướng ngược với hướng của $\overrightarrow{MD}$ và có độ lớn |$\overrightarrow{F3}$| = |-$\overrightarrow{MD}$| = 100√3 .

Bình luận