Giải bài 3.9 bài hệ thức lượng trong tam giác
Bài tập 3.9. Trên nóc một tòa nhà có một ăng-ten cao 5m. Từ một vị trí quan sát A cao 7m so với mặt đất có thể nhìn thấy đỉnh B và chân C của cột ăng-ten, với các góc tương ứng là 50o và 40o so với phương nằm ngang.
a. Tính các góc của tam giác ABC.
b. Tính chiều cao của tòa nhà.
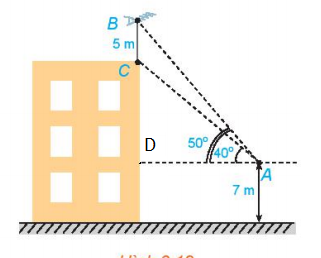
a. Gọi D là hình chiếu của A lên tòa nhà.
Xét tam giác CDA vuông tại D có: C = 90o – A = 50o
Suy ra góc BCA = 130o
Ta có: $\widehat{CAB}=50^{o}-40^{o}=10^{o}$
$\widehat{CBA}=180^{o}-10^{o}-130^{o}=40^{o}$
b.
- Áp dụng định lí sin trong tam giác ABC, ta có: $\frac{a}{sin A}=\frac{b}{sin B}=\frac{c}{sin C}$
$\frac{BC}{sin A}=\frac{AC}{sin B}$
$\Rightarrow AC \approx 18,5$
- Xét tam giác CDA vuông tại D có: CD = AC.sin 40o = 11,9$ m
- Chiều cao của tòa nhà là: 7 + 11,9 = 18,9 m.
Xem toàn bộ: Giải bài 6 Hệ thức lượng trong tam giác

Bình luận