Cho đường thẳng d đi qua trung điểm M của đoạn thẳng AB và không vuông góc với AB.
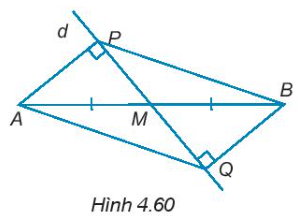
4.58. Cho đường thẳng d đi qua trung điểm M của đoạn thẳng AB và không vuông góc với AB. Kẻ AP, BQ (P $\in $ d, Q $\in $ d) vuông góc với đường thẳng d (H.4.60). Chứng minh rằng:
a) AP = BQ.
b) $\Delta APB=\Delta BQA$
a) Xét tam giác vuông PAM và tam giác vuông QBM có:
AM = BM (do M là trung điểm của AB)
$\widehat{PMA}=\widehat{QMB}$ (hai góc đối đỉnh)
Do đó, $\Delta PAM = \Delta QBM$ (cạnh huyền – góc nhọn).
Suy ra AP = BQ.
b) Xét tam giác APB và tam giác BQA có:
AP = BQ (cmt)
$\widehat{PAB}=\widehat{QBA}$ (do $\Delta PAM=\Delta QBM)$
AB: cạnh chung
Do đó, $\Delta APB = \Delta BQA $
Xem toàn bộ: Giải SBT toán 7 Kết nối tri thức Ôn tập chương IV

Bình luận