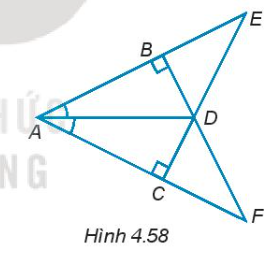
Cho các điểm A, B, C, D, E, F như Hình 4.58.
4.56. Cho các điểm A, B, C, D, E, F như Hình 4.58.
a) Tìm ba cặp tam giác vuông bằng nhau và giải thích vì sao chúng bằng nhau.
b) Chứng minh $\Delta ADE=\Delta ADF$.
a) Xét tam giác vuông ABD và tam giác vuông ACD có:
AD: cạnh chung
$\widehat{BAD}=\widehat{CAD}$ (gt)
Do đó, $\Delta ABD = \Delta ACD$ (cạnh huyền – góc nhọn).
Xét tam giác vuông ABF và tam giác vuông ACE có:
AB = AC (do $\Delta ABD = \Delta ACD$)
$\widehat{FAB}=\widehat{EAC}$ (góc chung)
Do đó, $\Delta ABF = \Delta ACE$ (cạnh góc vuông và góc nhọn kề).
Xét tam giác vuông BDE và tam giác vuông CDF có:
BD = CD (do $\Delta ABD = \Delta ACD$)
$\widehat{BDE}=\widehat{CDF}$ (hai góc đối đỉnh)
Do đó, $\Delta BDE = \Delta CDF$ (cạnh góc vuông và góc nhọn kề).
Vậy ta có ba cặp tam giác vuông bằng nhau như trên.
b) Xét tam giác ADE và tam giác ADF có:
AE = AF (do $\Delta ABF = \Delta ACE$)
$\widehat{EAD}=\widehat{FAD}$ (gt)
AD: cạnh chung
Do đó, $\Delta ADE = \Delta ADF$ (c.g.c)
Xem toàn bộ: Giải SBT toán 7 Kết nối tri thức Ôn tập chương IV

Bình luận