Bài tập file word mức độ vận dụng bài 10: Tứ giác
3. VẬN DỤNG (4 câu)
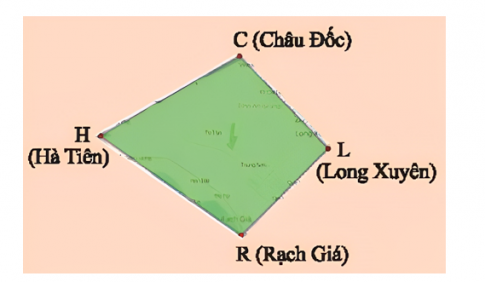
Câu 1: Tìm các đỉnh, cạnh và đường chéo của tứ giác Long Xuyên CHRL
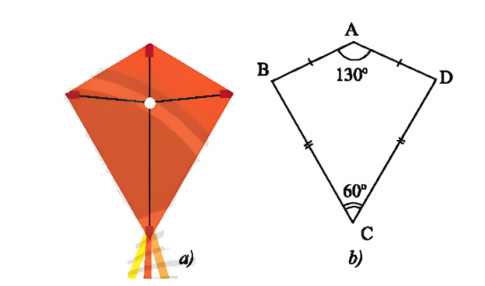
Câu 2: Phần thân của cái diều ở Hình a được vẽ lại như Hình b. Tìm số đo các góc chưa biết trong hình.
Câu 3. Ta có tứ giác ABCD với AB = AD, CB = CD (Hình vẽ) là hình "cái diều".
a) Chứng minh rằng AC là đường trung trực của BD
b) Cho biết $\widehat{B}=95^{\circ},\widehat{C}=35^{\circ}$. Tính $\widehat{A}$ và $\widehat{D}$

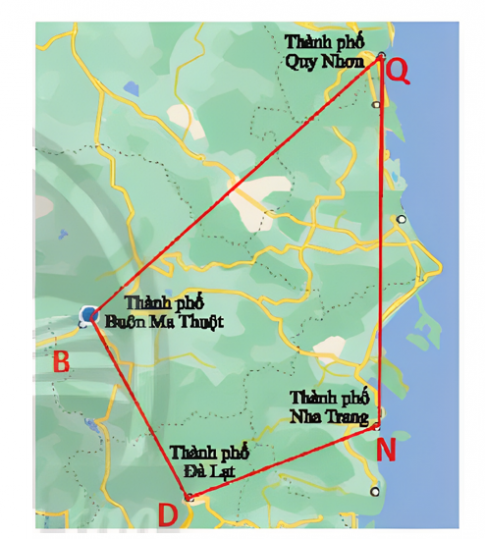
Bài 4. Trên bản đồ, tứ giác BDNQ với các đỉnh là các thành phố Buôn Ma Thuột, Đà Lạt, Nha Trang, Quy Nhơn.
a) Tìm các cạnh kề và cạnh đối của cạnh BD
b) Tìm các đường chéo của tứ giác
Câu 1:
Các đỉnh: C, H, R, L
Các cạnh: CH, HR, RL, CL
Các đường chéo: CR, HL
Câu 2:
Xét tam giác ABC và ADC ta có:
AB = AD
BC = CD
AC chung
Suy ra $\Delta ABC=\Delta ADC$ (c.c.c)
⇒$\widehat{ABC}=\widehat{ADC}$
Xét tứ giác ABCD có:
$\widehat{ABC}+\widehat{ADC}+\widehat{BAD}+\widehat{BCD}$
$=360^{\circ}$
$\widehat{ABC}=\widehat{ADC}$
$=\left [ 360^{\circ}-(130^{\circ}+60^{\circ}) \right ]:2=85^{\circ}$
Câu 3.
a) Ta có: AB = AD (gt) =>A thuộc đường trung trực của BD
CB = CD (gt) => C thuộc đường trung trực của BD.
Vậy AC là đường trung trực của BD.
b) Xét ∆ ABC và ∆ADC có:
AB = AD (gt)
CB = CD (gt)
AC chung
nên ∆ABC = ∆ADC (c.c.c)
Suy ra $\widehat{B}=\widehat{D}=95^{\circ}$
Ta có: $\widehat{A}=360-(95^{\circ}+95^{\circ}+35^{\circ})=135^{\circ}$
Bài 4.
a) Cạnh kề cạnh BD: DN, BQ
Cạnh đối cạnh BD: NQ
b) Các đường chéo: BN, DQ
Xem toàn bộ: Bài tập file word Toán 8 Kết nối bài 10: Tứ giác

Bình luận