Bài tập file word mức độ thông hiểu bài 10: Tứ giác
2. THÔNG HIỂU (7 câu)
Câu 1. Tìm x trong mỗi tứ giác sau:

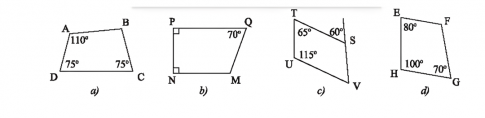
Câu 2. Tìm số đo các góc chưa biết của tứ giác trong hình:
Câu 3: Góc kề bù với một góc của tứ giác được gọi là góc ngoài của tứ giác đó.
Hãy tính tổng số đo bốn góc ngoài $ \widehat{A_{1}}, \widehat{B_{1}}, \widehat{C_{1}},\widehat{D_{1}}$ của tứ giác ABCD ở hình.

Câu 4: Tứ giác ABCD có $ \widehat{A}=100^{\circ}$ , góc ngoài tại đỉnh B bằng 110∘, $ \widehat{C}=75^{\circ}$. Tính số đo góc D
Câu 5: Tứ giác ABCD có góc ngoài tại đỉnh A bằng 65∘, góc ngoài tại đỉnh B bằng 100∘, góc ngoài tại đỉnh C bằng 60∘. Tính số đo góc ngoài tại đỉnh D

Câu 6. Tứ giác ABCD có số đo $ \widehat{A}=x, \widehat{B}=2x, \widehat{C}=3x, \widehat{D}=4x$. Tính số đo các góc của tứ giác đó.
Câu 7.
a) Tứ giác .ABCD có $ \widehat{A}+\widehat{C}=180^{\circ}$ thì $ \widehat{B}+\widehat{D}$ bằng bao nhiêu độ?
b) Có hay không một tứ giác có 2 góc tù và 2 góc vuông?
c) Có hay không một tứ giác có cả 4 góc đều là góc nhọn?
Câu 1.
Do tổng số đo bốn góc của một tứ giác bằng 360∘ nên ta có:
Trong tứ giác PSRQ: $x+2x+70^{\circ}+80^{\circ}=360^{\circ}$ , suy ra $3x=210^{\circ}$, do đó $x=70^{\circ}$
Trong tứ giác ABCD: $x=360^{\circ}-(95^{\circ}+100^{\circ}+90^{\circ})$ , suy ra $x=75^{\circ}$
Trong tứ giác EFGH: $x=360^{\circ}-(99^{\circ}+90^{\circ}+90^{\circ})$, suy ra x = 81o
Câu 2.
Tổng các góc trong tứ giác bằng $360^{\circ}$ nên ta có:
a) Trong tứ giác ABCD: $\widehat{B}=360^{\circ}-(100^{\circ}+75^{\circ}+75^{\circ})=100^{\circ}$
b) Trong tứ giác MNPQ: $\widehat{M}=360^{\circ}-(90^{\circ}+90^{\circ}+70^{\circ})=110^{\circ}$
c) Trong tứ giác STUV: $\widehat{S}=180^{\circ}-60^{\circ}=120^{\circ}$
$\widehat{V}=360^{\circ}-(120^{\circ}+65^{\circ}+115^{\circ})=60^{\circ}$
d) Trong tứ giác EFGH:
$\widehat{F}=360^{\circ}-(70^{\circ}+100^{\circ}+80^{\circ})=110^{\circ}$
Câu 3:
Ta có:
$\widehat{A_{1}}+\widehat{A}=180^{\circ}\Rightarrow \widehat{A_{1}}=180^{\circ}-A$
$\widehat{B_{1}}+\widehat{B}=180^{\circ}\Rightarrow \widehat{B_{1}}=180^{\circ}-B$
$\widehat{C_{1}}+\widehat{C}=180^{\circ}\Rightarrow \widehat{C_{1}}=180^{\circ}-C$
$\widehat{D_{1}}+\widehat{D}=180^{\circ}\Rightarrow \widehat{D_{1}}=180^{\circ}-D$
$\Rightarrow \widehat{A_{1}}+\widehat{B_{1}}+\widehat{C_{1}}+\widehat{D_{1}}=180^{\circ}-\widehat{A}+180^{\circ}-\widehat{B}+180^{\circ}-\widehat{C}+180^{\circ}-\widehat{D}$
$=4.180^{\circ}-(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D})$
Mà theo định lý tổng bốn góc trong một tứ giác bằng 360º ta có:
$\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^{\circ}$
$\Rightarrow \widehat{A_{1}}+ \widehat{B_{1}}+ \widehat{C_{1}}+ \widehat{D_{1}}=4.180^{\circ}-360^{\circ}$
Câu 4:
Ta có: $\widehat{B}=180^{\circ}-110^{\circ}=70^{\circ}$
Do tổng các góc của một tứ giác bằng $360^{\circ}$ nên ta có:
$D=360^{\circ}-(100^{\circ}+70^{\circ}+75^{\circ}=115^{\circ})$
Câu 5:
Ta có: $\widehat{BAD}+A_{ngoai}=180^{\circ}$ (hai góc kề bù)
Do đó: $\widehat{BAD}+65^{\circ}=180^{\circ}\Rightarrow \widehat{BAD}=180^{\circ}-65^{\circ}=115^{\circ}$
$\widehat{ABC}+B_{ngoai}=180^{\circ}$ (hai góc kề bù)
Do đó: $\widehat{ABC}+100^{\circ}=180^{\circ}\Rightarrow \widehat{ABC}=180^{\circ}-100^{\circ}=80^{\circ}$
$\widehat{BCD}+C_{ngoai}=180^{\circ}$ (hai góc kề bù)
Do đó: $\widehat{BCD}+60^{\circ}=180^{\circ}\Rightarrow \widehat{BCD}=180^{\circ}-60^{\circ}=120^{\circ}$
Tứ giác ABCD có: $\widehat{BAD}+\widehat{ABC}+\widehat{BCD}+\widehat{ADC}=360^{\circ}$
Do đó:
$115^{\circ}+80^{\circ}+120^{\circ}+\widehat{ADC}=360^{\circ}\Rightarrow \widehat{ADC}=360^{\circ}-(115^{\circ}+80^{\circ}+120^{\circ})=45^{\circ}$
Ta có $D_{ngoai}+\widehat{ADC}=180^{\circ}$ (hai góc kề bù)
Do đó $D_{ngoai}+45^{\circ}=180^{\circ}\Rightarrow D_{ngoai}=180^{\circ}-45^{\circ}=135^{\circ}$
Vậy góc ngoài tại đỉnh D bằng $135^{\circ}$
Câu 6.
Tứ giác ABCD có:
$\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^{\circ}$
hay $x+2x+3x+4x=360^{\circ}$
$\Rightarrow 10x=360^{\circ}\Rightarrow x=36^{\circ}$
Vậy
Câu 7.
a) Tứ giác ABCD có $\widehat{A}+\widehat{C}=180^{\circ}$ thì $\widehat{B}+\widehat{D}=360^{\circ}-(\widehat{A}+\widehat{C})$
b) Không có một tứ giác nào có 2 góc tù và 2 góc vuông.
c) Không có một tứ giác nào mà có cả 4 góc đều là góc nhọn.
Xem toàn bộ: Bài tập file word Toán 8 Kết nối bài 10: Tứ giác

Bình luận